Difference between revisions of "Csőtápvonal"
(→A szimulációval kapott eredmények) |
|||
| (25 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
| width=50% | | | width=50% | | ||
''' ''' | ''' ''' | ||
| + | |- | ||
| + | | style="text-align: left; width: 36%;" | | ||
| + | '''Oktató''' | ||
| + | * [http://wiki.maxwell.sze.hu/index.php/Marcsa Marcsa Dániel] (óraadó) | ||
| + | * Előadás: - | ||
| + | * Fogadóóra: egyeztetés alapján | ||
| + | | style="text-align: left; width: 36%;" | | ||
| + | '''További oktatók:''' | ||
| + | * - | ||
| + | * Fogadóóra: -. | ||
|} | |} | ||
=== A feladat célja === | === A feladat célja === | ||
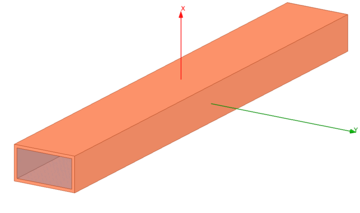
| − | [[File:Waveguide Geometry.png| | + | [[File:Waveguide Geometry.png|360px|thumb|right|alt=A feladat geometriája. | A feladat geometriája.]] |
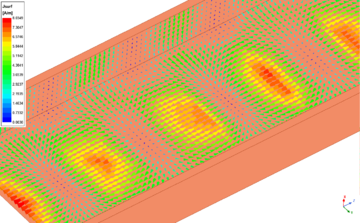
| + | [[File:TE10 WallCurrent.png|360px|thumb|right|alt=A kialakuló faláramok a négyszögletes hullámvezetőben. | A kialakuló faláramok a négyszögletes hullámvezetőben.]] | ||
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása egy négyszög keresztmetszetű csőtápvonal esetében. A szimuláció beállításai és eredményei elősegítsék a más tárgyakból tanult elméleti ismeretek elmélyülését. | A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása egy négyszög keresztmetszetű csőtápvonal esetében. A szimuláció beállításai és eredményei elősegítsék a más tárgyakból tanult elméleti ismeretek elmélyülését. | ||
| Line 33: | Line 44: | ||
A geometria elkészítését és a beállításokat a feladathoz készült YouTube videóban részletezem. | A geometria elkészítését és a beállításokat a feladathoz készült YouTube videóban részletezem. | ||
| − | Azonban egy csőtápvonal szimulációja előtt érdemes meghatározni a vágási frekvenciát (vagy határfrekvenciát, ami alatt nincs hullámterjedés a csőtápvonalban). A vágási frekvencia a következő összefüggéssel határozható meg <ref name="MikroTech1"> Kolos T., Standeisky I.: ''Mikrohullámú technika I.'', Tankönyvkiadó, 1980 | + | A feladat megoldásához az elektromos térerősségre felírt Helmholtz-egyenletet<ref name="Istvanffy"> Istvánffy E.: ''Tápvonalak, antennák és hullámterjedés'', Műegyetemi Kiadó, 1997. </ref> oldjuk meg |
| + | ::<math> \Delta\vec{E} + k^2\vec{E} = 0 </math> | ||
| + | ahol <math>k = \omega\sqrt{\mu\varepsilon}</math> a terjedési együttható és <math>\Delta</math> a [https://hu.wikipedia.org/wiki/Laplace-oper%C3%A1tor Laplace-operátor]. | ||
| + | |||
| + | Azonban egy csőtápvonal szimulációja előtt érdemes meghatározni a vágási frekvenciát (vagy határfrekvenciát, ami alatt nincs hullámterjedés a csőtápvonalban). A vágási frekvencia a következő összefüggéssel határozható meg<ref name="Istvanffy"></ref><ref name="MikroTech1"> Kolos T., Standeisky I.: ''Mikrohullámú technika I.'', Tankönyvkiadó, 1980. </ref>: | ||
::<math> f_{h,mn} = \frac{1}{2\sqrt{\mu\varepsilon}}\sqrt{\left(\frac{m}{a}\right)^2 + \left(\frac{n}{b}\right)^2}</math>, | ::<math> f_{h,mn} = \frac{1}{2\sqrt{\mu\varepsilon}}\sqrt{\left(\frac{m}{a}\right)^2 + \left(\frac{n}{b}\right)^2}</math>, | ||
ahol <math>\mu</math> és <math>\varepsilon</math> a csőtápvonalat kitöltő dielektrikum permeabilitása és permittivitása. | ahol <math>\mu</math> és <math>\varepsilon</math> a csőtápvonalat kitöltő dielektrikum permeabilitása és permittivitása. | ||
| + | |||
| + | == A szimulációval kapott eredmények == | ||
| + | [[File:S11S21 Parameter.png|500px|thumb|right|alt=A bemeneti reflexió (<math>\text{S}_{11}</math> paraméter) és az előre irányú átviteli tényező (<math>\text{S}_{21}</math> paraméter) a frekvencia függvényében. | A bemeneti reflexió (<math>\text{S}_{11}</math> paraméter) és az előre irányú átviteli tényező (<math>\text{S}_{21}</math> paraméter) a frekvencia függvényében.]] | ||
A levegővel kitöltött csőtápvonalnál <math>\text{TE}_{10}</math> (ejtsd: ''té e egy nulla'') módus esetében a vágási frekvencia | A levegővel kitöltött csőtápvonalnál <math>\text{TE}_{10}</math> (ejtsd: ''té e egy nulla'') módus esetében a vágási frekvencia | ||
::<math> f_{h,10} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}}\sqrt{\left(\frac{1}{0,02}\right)^2 + \left(\frac{0}{0,01}\right)^2} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}\cdot0,02}= 7,4926\text{GHz} \approx 7,5\text{GHz}</math>. | ::<math> f_{h,10} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}}\sqrt{\left(\frac{1}{0,02}\right)^2 + \left(\frac{0}{0,01}\right)^2} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}\cdot0,02}= 7,4926\text{GHz} \approx 7,5\text{GHz}</math>. | ||
| − | + | A bemeneti reflexió és az előre irányú átviteli tényező frekvenciafüggvényén (jobb oldali ábra) jól látható, hogy a szimulációval visszakaptuk az előzőleg analitikusan kiszámolt vágási frekvenciát. A vágási frekvenciát követően az átvitel eléri a maximumát. | |
| − | |||
| − | |||
| − | |||
| − | Emellett a lenti ábrákon látható az elektromos (baloldali ábra - E field) és mágneses (jobboldali ábra - H field) térerősség a négyszögletes csőtápvonal keresztmetszetében <math>\text{TE}_{10}</math> módusnál. Ezekhez tartozik a két animáció, amelyből látható, hogy az elektromos térerősségnek csak a terjedési irányra merőleges komponense van (<math> E_z = 0 </math>), vagyis itt tényleg egy transzverzális elektromos (<math> TE </math>) térről van szó. | + | Emellett a lenti ábrákon látható az elektromos (baloldali ábra - E field) és mágneses (jobboldali ábra - H field) térerősség a négyszögletes csőtápvonal keresztmetszetében <math>\text{TE}_{10}</math> módusnál. Ezekhez tartozik a két animáció, amelyből látható, hogy az elektromos térerősségnek csak a terjedési irányra merőleges komponense van (<math> E_z = 0 </math>), vagyis itt tényleg egy transzverzális elektromos (<math>\text{TE}</math>) térről van szó. |
{| width=100% | {| width=100% | ||
Latest revision as of 19:57, 28 January 2020
|
Négyszög keresztmetszetű csőtápvonal (Rectangular waveguide) | |
|
|
|
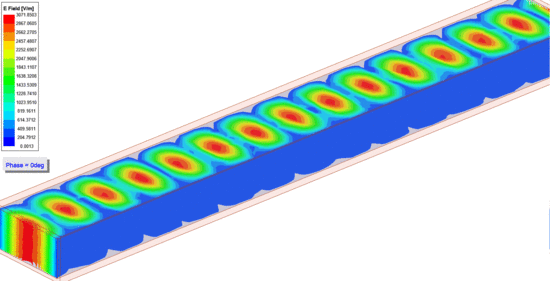
| Négyszög keresztmetszetű csőtápvonal. | Az elektromos térerősség terjedése a csőtápvonalban. [Kattints a képre az animáció megtekintéséhez.] |
|
| |
|
Oktató
|
További oktatók:
|
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása egy négyszög keresztmetszetű csőtápvonal esetében. A szimuláció beállításai és eredményei elősegítsék a más tárgyakból tanult elméleti ismeretek elmélyülését.
A feladat megoldása során azzal nem foglalkozunk, milyen módon lehet a csőtápvonalba jelet juttatni.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A Maxwell-egyenletek teljes rendszerének ismerete (hullámegyenlet ismerete);
- Csőtápvonal működésének ismeret.
A vizsgált csőtápvonal
A feladat geometriai méretei: [math]a = 2\text{cm}[/math] (széles oldal); [math]b = 1\text{cm}[/math] (keskeny oldal); [math]L = 16\text{cm}; th = 1\text{mm}[/math] (csőtápvonal falvastagsága).
A geometria elkészítését és a beállításokat a feladathoz készült YouTube videóban részletezem.
A feladat megoldásához az elektromos térerősségre felírt Helmholtz-egyenletet[1] oldjuk meg
- [math] \Delta\vec{E} + k^2\vec{E} = 0 [/math]
ahol [math]k = \omega\sqrt{\mu\varepsilon}[/math] a terjedési együttható és [math]\Delta[/math] a Laplace-operátor.
Azonban egy csőtápvonal szimulációja előtt érdemes meghatározni a vágási frekvenciát (vagy határfrekvenciát, ami alatt nincs hullámterjedés a csőtápvonalban). A vágási frekvencia a következő összefüggéssel határozható meg[1][2]:
- [math] f_{h,mn} = \frac{1}{2\sqrt{\mu\varepsilon}}\sqrt{\left(\frac{m}{a}\right)^2 + \left(\frac{n}{b}\right)^2}[/math],
ahol [math]\mu[/math] és [math]\varepsilon[/math] a csőtápvonalat kitöltő dielektrikum permeabilitása és permittivitása.
A szimulációval kapott eredmények
![A bemeneti reflexió ([math]\text{S}_{11}[/math] paraméter) és az előre irányú átviteli tényező ([math]\text{S}_{21}[/math] paraméter) a frekvencia függvényében.](/index.php/File:S11S21_Parameter.png)
A levegővel kitöltött csőtápvonalnál [math]\text{TE}_{10}[/math] (ejtsd: té e egy nulla) módus esetében a vágási frekvencia
- [math] f_{h,10} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}}\sqrt{\left(\frac{1}{0,02}\right)^2 + \left(\frac{0}{0,01}\right)^2} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}\cdot0,02}= 7,4926\text{GHz} \approx 7,5\text{GHz}[/math].
A bemeneti reflexió és az előre irányú átviteli tényező frekvenciafüggvényén (jobb oldali ábra) jól látható, hogy a szimulációval visszakaptuk az előzőleg analitikusan kiszámolt vágási frekvenciát. A vágási frekvenciát követően az átvitel eléri a maximumát.
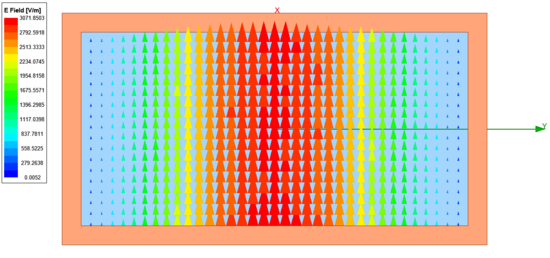
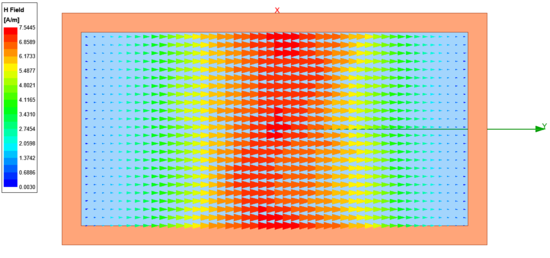
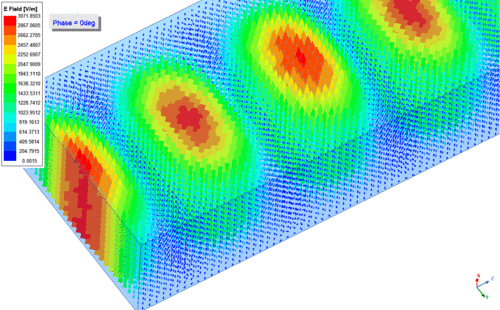
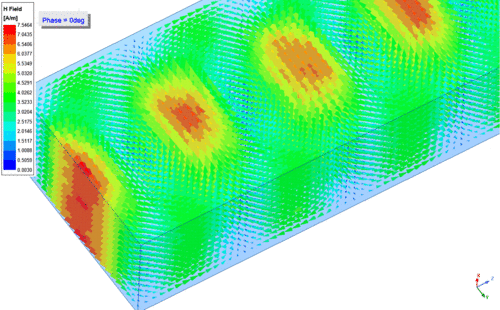
Emellett a lenti ábrákon látható az elektromos (baloldali ábra - E field) és mágneses (jobboldali ábra - H field) térerősség a négyszögletes csőtápvonal keresztmetszetében [math]\text{TE}_{10}[/math] módusnál. Ezekhez tartozik a két animáció, amelyből látható, hogy az elektromos térerősségnek csak a terjedési irányra merőleges komponense van ([math] E_z = 0 [/math]), vagyis itt tényleg egy transzverzális elektromos ([math]\text{TE}[/math]) térről van szó.
|
|
|
| Az elektromos térerősség vektorok a bemeneti portnál [math]\text{TE}_{10}[/math] módus esetében. | A mágneses térerősség vektorok a bemeneti portnál [math]\text{TE}_{10}[/math] módus esetében. |
|
|
|
| Az elektromos térerősség vektorok a csőtápvonalban [math]\text{TE}_{10}[/math] módus esetében.[Kattints a képre az animáció megtekintéséhez.] | A mágneses térerősség vektorok a csőtápvonalban [math]\text{TE}_{10}[/math] módus esetében.[Kattints a képre az animáció megtekintéséhez.] |
