Difference between revisions of "2. lecke példája"
| (71 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
[[Image:InductionHeating.jpg|450px]] | [[Image:InductionHeating.jpg|450px]] | ||
| align=center | | | align=center | | ||
| − | [[ | + | [[File:InductionHeating Maxwell3.gif|600px]] |
| + | |- | ||
| + | |align=center | <span style="font-size:88%;">'''Egy fém indukciós hevítése a valóságban.'''</span><ref>Induction heating - https://en.wikipedia.org/wiki/Induction_heating</ref> | ||
| + | |align=center | <span style="font-size:88%;">'''Egy fém indukciós hevítés szimulációval.'''</span> <span style="font-size:80%; color:blue;">[Kattints a képre az animáció megtekintéséhez.]</span> | ||
|- valign=top | |- valign=top | ||
| width=50% | | | width=50% | | ||
| + | ''' ''' | ||
| + | |- | ||
| + | | style="text-align: left; width: 36%;" | | ||
'''Oktató''' | '''Oktató''' | ||
| − | * Marcsa Dániel (óraadó) | + | * [http://wiki.maxwell.sze.hu/index.php/Marcsa Marcsa Dániel] (óraadó) |
| − | * Előadás: | + | * Előadás: - |
* Fogadóóra: egyeztetés alapján | * Fogadóóra: egyeztetés alapján | ||
| − | | width | + | | style="text-align: left; width: 36%;" | |
'''További oktatók:''' | '''További oktatók:''' | ||
* - | * - | ||
| Line 28: | Line 34: | ||
=== A feladat megoldásának lépései === | === A feladat megoldásának lépései === | ||
| − | Az ANSYS Electronics Desktop elindítását követően a menüből kiválasztjuk a ''Project -> Insert Maxwell 3D Design'' almenüt. <br /> A következőkben bemutatott lépésektől eltérően is megvalósítható a feladat. Az ANSYS Maxwell használatához a ''Help'' menüje és a ''YouTube''-on fellelhető videók sok segítséget nyújtanak. | + | Az ANSYS Electronics Desktop elindítását követően a menüből kiválasztjuk a ''Project -> Insert Maxwell 3D Design'' almenüt. <br /> A következőkben bemutatott lépésektől eltérően is megvalósítható a feladat. Az [https://www.ansys.com/products/electronics/ansys-maxwell ANSYS Maxwell] használatához a ''Help'' menüje és a ''YouTube''-on fellelhető videók sok segítséget nyújtanak. |
== A geometria elkészítése == | == A geometria elkészítése == | ||
| − | Ebben az esetben egy előre elkészített geometriával dolgozunk. Ez annak felel meg, amikor egy tervező már elkészítettet a | + | Ebben az esetben egy előre elkészített geometriával dolgozunk. Ez annak felel meg, amikor egy tervező már elkészítettet a geometriát, amit a szimulációs mérnök használ az eszköz számítógépes vizsgálatánál.<br/> |
| + | Tehát ennél a feladatnál a geometria importálásra kerül. A geometria importálása a ''Modeler <math>\to</math> Import...'' menü segítségével lehetséges. | ||
| − | + | == A feladat beállításai == | |
| − | == Az anyagok definiálása == | + | === Az anyagok definiálása === |
Ebben a feladatban a hevítéshez használt tekercs anyaga ''réz'' (copper), a hevített vas ''öntöttvas'' (cast iron) és még definiálni kell a tekercset és vasat körülvevő ''levegőt'' (air). | Ebben a feladatban a hevítéshez használt tekercs anyaga ''réz'' (copper), a hevített vas ''öntöttvas'' (cast iron) és még definiálni kell a tekercset és vasat körülvevő ''levegőt'' (air). | ||
| − | == A gerjesztés megadása == | + | A levegő definiálásához a legegyszerűbb a ''Region''-t használni, ahol |
| + | |||
| + | {| class="wikitable" style="text-align: center;" | ||
| + | |- | ||
| + | | +X Padding | ||
| + | | -X Padding | ||
| + | | +Y Padding | ||
| + | | -Y Padding | ||
| + | | +Z Padding | ||
| + | | -Z Padding | ||
| + | |- | ||
| + | | 0% | ||
| + | | 75% | ||
| + | | 160% | ||
| + | | 160% | ||
| + | | 100% | ||
| + | | 100% | ||
| + | |} | ||
| + | |||
| + | === A gerjesztés megadása === | ||
| + | A gerjesztés a tekercs két kivezetésének felületére kell definiálni. A gerjesztés 50A, amelyet a tekercs kivezetéseinek felületére kell definiálni. A definiálásnál arra kell ügyelni, hogy az egyik felületen befelé, a másik feleületen kifelé adjuk meg a gerjesztés irányát. | ||
| + | |||
| + | === A hálózási beállítások === | ||
| + | [[File:InductionHeating FEMMesh.png|360px|thumb|left|alt=Az öntöttvas rúd és a tekercs diszkretizálása.|Az öntöttvas rúd és a tekercs diszkretizálása.]] | ||
| + | |||
| + | Az ''Eddy Current'' megoldás típusnál a megoldó adaptívan sűríti a hálót. Azonban olyan esetekben, amikor az örvényáram jelentős lehet, célszerű a ''Skin Depth Based...'' hálózási műveletet alkalmazni azokra a felületekre, ahol ez szükséges. | ||
| + | |||
| + | Az öntöttvas rúd felületére alkalmaztam ezt a hálózást, ahogy az ábrán is látható. Az ANSYS Maxwell 2019R1-es verziójától kezdve az adaptív hálózó nem változtatja a felbontás azokon a részeken, ahol a ''Skin Depth Based...'' műveletet definiáltuk. Ennek a célja a gyorsabb konvergencia, azonban emiatt fontos a felbontás megfelelő definiálása a behatolási mélységben. | ||
== A megoldó beállítása, a szimuláció futtatása == | == A megoldó beállítása, a szimuláció futtatása == | ||
| + | |||
| + | Ahogy a hálózási beállításoknál írtam, adaptívan sűríti a szükséges helyeken a megoldó a felbontást. Azonban az adaptív hálósűrítés paramétereit a megoldónál kell beállítani. Az adaptív lépések maximális száma (''Maximum Number of Passes'') legyen 10, a hibahatár (''Percent Error'') pedig 0,5%. A finomítás mértékét adaptív lépésenként (''Refinement Per Pass'') háromdimenziós feladat esetében célszerű az alapértékről (30%) lejjebb venni. Ez különösen akkor igaz, ha nincs előzetes információnk, hogy milyen módon konvergál, hogyan csökken a hiba a példa esetében. A finomítás mértéke 20% legyen. A megoldónál lehet a gerjesztés frekvenciáját (''Adaptive Frequency'') megadni, ennél a példánál <math>f = 500~\text{Hz}</math>. | ||
| + | |||
| + | Az előző beállítások mellett még lehetőség van a nemlineáris maradékot (''Nonlinear Residual'') beállítani, de a példa esetében minden anyag lineár mágnesezési karakterisztikával rendelkezik. Ha szükséges itt lehet a direkt megoldó helyett bekapcsolni az iteratív megoldót, ahol szintén definiálni kell a leállási kritériumként szolgáló hibát (''Relative Residual''). Az adaptív hálósűrítés mellett, ennél a feladattípusnál lehetőség van magasabb fokú formafüggvények használatára (''Use higher order shape functions''), illetve ha szükséges a frekvenciasöprés (''Frequency Sweep'') tartományát és az ahhoz tartozó lépésközt. | ||
== Az eredmények kiértékelése == | == Az eredmények kiértékelése == | ||
| + | |||
| + | Az 1. lecke példájánál látott változókon (induktivitás, erő) túl meghatározhatjuk a vasdarabban, a tekercsben létrejövő veszteségeket. Ezek a mennyiségek a frekvencia függvényében (''Frequency Sweep'' lehetősége) is vizsgálhatóak. | ||
| + | |||
| + | Az [https://www.ansys.com/products/electronics/ansys-maxwell ANSYS Maxwell] automatikusan kiszámítja a veszteségeket a feladatban, azonban ha arra vagyunk kíváncsiak, egy-egy térrészben (pl. az öntöttvas rúdban) mekkora az örvényáram okozta veszteség, akkor azt nekünk kell kiszámolni a ''Calculator'' (Maxwell 3D <math>\to</math> Fields <math>\to</math> Calculator...) segítségével. Az örvényáramú veszteség a következő összefüggéssel számítható | ||
| + | |||
| + | ::<math> P_{ö} = \frac{1}{2}\int_{V} \vec{J}\cdot\vec{E}^{*}\,\text{d}V = \int_{V} \frac{\vec{J}\cdot\vec{J}^{*}}{2\sigma}\,\text{d}V\quad[\text{W}]</math>. | ||
| + | |||
| + | Azonban a fenti összefüggés helyett a ''Calculator''-ban a következő lépéseket kell elvégezni | ||
| + | |||
| + | * <span style="font-family:Courier;">Input</span> <math>\to</math> <span style="font-family:Courier;">Quantity</span> <math>\to</math> <span style="font-family:Courier;">OhmicLoss</span> | ||
| + | * <span style="font-family:Courier;">Input</span> <math>\to</math> <span style="font-family:Courier;">Geometry</span> <math>\to</math> ''Itt kiválasztjuk a térfogatot, ahol számolni szeretnénk a veszteséget'' | ||
| + | * <span style="font-family:Courier;">Scalar</span> <math>\to</math> <math>\int</math> (''Integrálás'') | ||
| + | * <span style="font-family:Courier;">Output</span> <math>\to</math> <span style="font-family:Courier;">Eval</span> | ||
| + | |||
| + | A térváltozók is megjeleníthetőek különböző formában erre mutat egy-egy példát a következő két ábra. | ||
| + | |||
| + | {| width=100% | ||
| + | |- | ||
| + | | align=center | | ||
| + | [[File:InductionHeating_HStreamlines.png|430px]] | ||
| + | | align=center | | ||
| + | [[File:InductionHeating OhmicLoss.png|530px]] | ||
| + | |- | ||
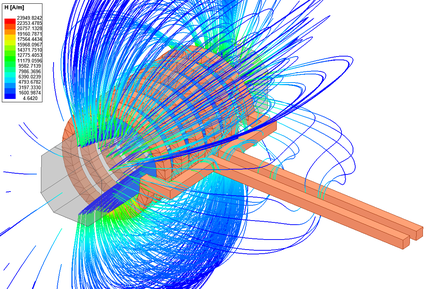
| + | |align=center | <span style="font-size:88%;">'''A tekercs körül kialakuló mágneses térerősség (''ANSYS Maxwell'').'''</span> | ||
| + | |align=center | <span style="font-size:88%;">'''Az örvényáram veszteség az öntöttvas rúd felületén (''ANSYS Maxwell'').'''</span> | ||
| + | |} | ||
| + | |||
| + | A feladat ''ANSYS Discovery AIM'' segítségével is megoldható, ahogy a következő két ábra mutatja. | ||
| + | |||
| + | {| width=100% | ||
| + | |- | ||
| + | | align=center | | ||
| + | [[File:InductionHeating_H_PlanesMagnitude.png|430px]] | ||
| + | | align=center | | ||
| + | [[File:InductionHeating_OhmicLoss_DiscoveryAIM.png|530px]] | ||
| + | |- | ||
| + | |align=center | <span style="font-size:88%;">'''A tekercs körül kialakuló mágneses térerősség (''ANSYS Discovery AIM'').'''</span> | ||
| + | |align=center | <span style="font-size:88%;">'''Az örvényáram veszteség az öntöttvas rúd felületén (''ANSYS Discovery AIM'').'''</span> | ||
| + | |} | ||
| + | |||
| + | == Irodalomjegyzék == | ||
| + | {{reflist}} | ||
Latest revision as of 20:01, 28 January 2020
|
Indukciós hevítés | |
| Egy fém indukciós hevítése a valóságban.[1] | Egy fém indukciós hevítés szimulációval. [Kattints a képre az animáció megtekintéséhez.] |
|
| |
|
Oktató
|
További oktatók:
|
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása egy örvényáramú szimuláción keresztül. Elősegítse az indukcióval történő olvasztás, hevítés és edzés fizikai hátterének mélyebb megismerését.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A kvázistacionárius mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához).
A feladat megoldásának lépései
Az ANSYS Electronics Desktop elindítását követően a menüből kiválasztjuk a Project -> Insert Maxwell 3D Design almenüt.
A következőkben bemutatott lépésektől eltérően is megvalósítható a feladat. Az ANSYS Maxwell használatához a Help menüje és a YouTube-on fellelhető videók sok segítséget nyújtanak.
A geometria elkészítése
Ebben az esetben egy előre elkészített geometriával dolgozunk. Ez annak felel meg, amikor egy tervező már elkészítettet a geometriát, amit a szimulációs mérnök használ az eszköz számítógépes vizsgálatánál.
Tehát ennél a feladatnál a geometria importálásra kerül. A geometria importálása a Modeler [math]\to[/math] Import... menü segítségével lehetséges.
A feladat beállításai
Az anyagok definiálása
Ebben a feladatban a hevítéshez használt tekercs anyaga réz (copper), a hevített vas öntöttvas (cast iron) és még definiálni kell a tekercset és vasat körülvevő levegőt (air).
A levegő definiálásához a legegyszerűbb a Region-t használni, ahol
| +X Padding | -X Padding | +Y Padding | -Y Padding | +Z Padding | -Z Padding |
| 0% | 75% | 160% | 160% | 100% | 100% |
A gerjesztés megadása
A gerjesztés a tekercs két kivezetésének felületére kell definiálni. A gerjesztés 50A, amelyet a tekercs kivezetéseinek felületére kell definiálni. A definiálásnál arra kell ügyelni, hogy az egyik felületen befelé, a másik feleületen kifelé adjuk meg a gerjesztés irányát.
A hálózási beállítások
Az Eddy Current megoldás típusnál a megoldó adaptívan sűríti a hálót. Azonban olyan esetekben, amikor az örvényáram jelentős lehet, célszerű a Skin Depth Based... hálózási műveletet alkalmazni azokra a felületekre, ahol ez szükséges.
Az öntöttvas rúd felületére alkalmaztam ezt a hálózást, ahogy az ábrán is látható. Az ANSYS Maxwell 2019R1-es verziójától kezdve az adaptív hálózó nem változtatja a felbontás azokon a részeken, ahol a Skin Depth Based... műveletet definiáltuk. Ennek a célja a gyorsabb konvergencia, azonban emiatt fontos a felbontás megfelelő definiálása a behatolási mélységben.
A megoldó beállítása, a szimuláció futtatása
Ahogy a hálózási beállításoknál írtam, adaptívan sűríti a szükséges helyeken a megoldó a felbontást. Azonban az adaptív hálósűrítés paramétereit a megoldónál kell beállítani. Az adaptív lépések maximális száma (Maximum Number of Passes) legyen 10, a hibahatár (Percent Error) pedig 0,5%. A finomítás mértékét adaptív lépésenként (Refinement Per Pass) háromdimenziós feladat esetében célszerű az alapértékről (30%) lejjebb venni. Ez különösen akkor igaz, ha nincs előzetes információnk, hogy milyen módon konvergál, hogyan csökken a hiba a példa esetében. A finomítás mértéke 20% legyen. A megoldónál lehet a gerjesztés frekvenciáját (Adaptive Frequency) megadni, ennél a példánál [math]f = 500~\text{Hz}[/math].
Az előző beállítások mellett még lehetőség van a nemlineáris maradékot (Nonlinear Residual) beállítani, de a példa esetében minden anyag lineár mágnesezési karakterisztikával rendelkezik. Ha szükséges itt lehet a direkt megoldó helyett bekapcsolni az iteratív megoldót, ahol szintén definiálni kell a leállási kritériumként szolgáló hibát (Relative Residual). Az adaptív hálósűrítés mellett, ennél a feladattípusnál lehetőség van magasabb fokú formafüggvények használatára (Use higher order shape functions), illetve ha szükséges a frekvenciasöprés (Frequency Sweep) tartományát és az ahhoz tartozó lépésközt.
Az eredmények kiértékelése
Az 1. lecke példájánál látott változókon (induktivitás, erő) túl meghatározhatjuk a vasdarabban, a tekercsben létrejövő veszteségeket. Ezek a mennyiségek a frekvencia függvényében (Frequency Sweep lehetősége) is vizsgálhatóak.
Az ANSYS Maxwell automatikusan kiszámítja a veszteségeket a feladatban, azonban ha arra vagyunk kíváncsiak, egy-egy térrészben (pl. az öntöttvas rúdban) mekkora az örvényáram okozta veszteség, akkor azt nekünk kell kiszámolni a Calculator (Maxwell 3D [math]\to[/math] Fields [math]\to[/math] Calculator...) segítségével. Az örvényáramú veszteség a következő összefüggéssel számítható
- [math] P_{ö} = \frac{1}{2}\int_{V} \vec{J}\cdot\vec{E}^{*}\,\text{d}V = \int_{V} \frac{\vec{J}\cdot\vec{J}^{*}}{2\sigma}\,\text{d}V\quad[\text{W}][/math].
Azonban a fenti összefüggés helyett a Calculator-ban a következő lépéseket kell elvégezni
- Input [math]\to[/math] Quantity [math]\to[/math] OhmicLoss
- Input [math]\to[/math] Geometry [math]\to[/math] Itt kiválasztjuk a térfogatot, ahol számolni szeretnénk a veszteséget
- Scalar [math]\to[/math] [math]\int[/math] (Integrálás)
- Output [math]\to[/math] Eval
A térváltozók is megjeleníthetőek különböző formában erre mutat egy-egy példát a következő két ábra.
| A tekercs körül kialakuló mágneses térerősség (ANSYS Maxwell). | Az örvényáram veszteség az öntöttvas rúd felületén (ANSYS Maxwell). |
A feladat ANSYS Discovery AIM segítségével is megoldható, ahogy a következő két ábra mutatja.
| A tekercs körül kialakuló mágneses térerősség (ANSYS Discovery AIM). | Az örvényáram veszteség az öntöttvas rúd felületén (ANSYS Discovery AIM). |
Irodalomjegyzék
- ↑ Induction heating - https://en.wikipedia.org/wiki/Induction_heating