Difference between revisions of "1. lecke példája"
| (209 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
|- | |- | ||
| align=center | | | align=center | | ||
| − | [[ | + | [[File:Injector3.gif|550px]] |
| align=center | | | align=center | | ||
| − | [[ | + | [[File:Pelda ResultsB.png|550px]] |
|- | |- | ||
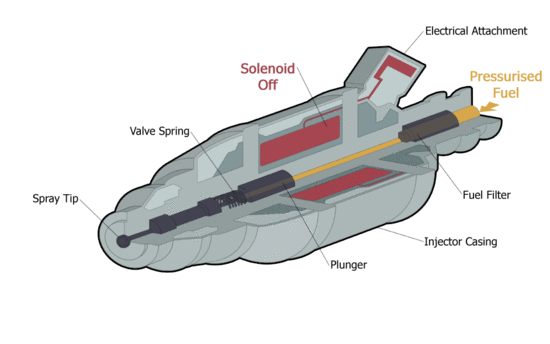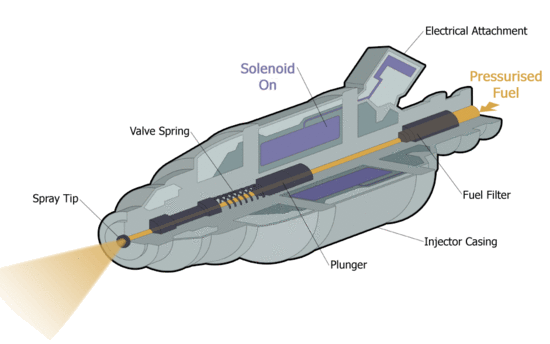
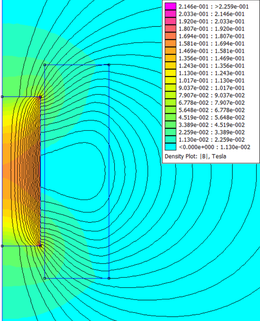
| − | |align=center | | + | |align=center | <span style="font-size:88%;">'''Az üzemanyag befecskendező működés közben.'''</span> <ref>https://upload.wikimedia.org/wikipedia/commons/2/29/Injector3.gif</ref> |
| − | |align=center | | + | |align=center | <span style="font-size:88%;">'''Az üzemanyag befecskendezőnél a B vektorok a szolenoid bekapcsolását követően.'''</span> |
|- valign=top | |- valign=top | ||
| width=50% | | | width=50% | | ||
| + | ''' ''' | ||
| + | |- | ||
| + | | style="text-align: left; width: 36%;" | | ||
'''Oktató''' | '''Oktató''' | ||
| − | * Marcsa Dániel (óraadó) | + | * [http://wiki.maxwell.sze.hu/index.php/Marcsa Marcsa Dániel] (óraadó) |
| − | * Előadás: | + | * Előadás: - |
* Fogadóóra: egyeztetés alapján | * Fogadóóra: egyeztetés alapján | ||
| − | | width | + | | style="text-align: left; width: 36%;" | |
'''További oktatók:''' | '''További oktatók:''' | ||
* - | * - | ||
| Line 29: | Line 32: | ||
* A végeselem-módszer lépései; | * A végeselem-módszer lépései; | ||
* A sztatikus mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához); | * A sztatikus mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához); | ||
| − | * A geometria elkészítéséhez CAD rendszer ismerete. | + | * A geometria elkészítéséhez CAD rendszer ismerete (háromdimenziós esetben). |
| − | + | == A feladat == | |
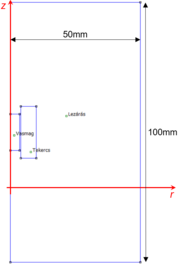
| − | + | [[File:Problem01_Definition_CrossSection.png|185px|thumb|left| |A feladat geometriának keresztmetszete és méretei.]] | |
| + | A vizsgált feladat (ha elhanyagoljuk a bekapcsoláskor fellépő átmeneti állapotot) állandósult állapotban sztatikus mágneses feladatnak tekinthető. A vasmag mozgásának (szelep nyitása / zárása) hatását is ennek megfelelően vizsgáljuk, vagyis minden pozícióhoz tartozik egy-egy szimuláció. Erre a különböző szoftverek más és más megoldást adnak (szkript, paramétervizsgálat). A mágnesszelep megoldása itt a FEMM és az ANSYS Discovery AIM Student szoftverekkel kerül bemutatásra, ezzel a féléves feladat elkészítéséhez is segítséget nyújtva. | ||
| − | + | '''A feladatban szereplő anyagok:''' | |
| − | + | * '''Vasmag:''' Nemlineáris mágnesezési görbével rendelkező acél ([https://drive.google.com/open?id=1hNmLPbkWXmyxgudRVMNpHXozw-OwUGly Steel1008]); | |
| + | * '''Tekercs:''' Anyaga réz (''Copper'') és 2000 menetes (''Number of Conductors''). Az áramerősség (''Current'') 0,2 A; | ||
| + | * '''Lezárás:''' Levegő (''Air''). | ||
| − | A | + | A feladat a mágnesszelep induktivitásának és a vasmagra ható erőnek a meghatározása. Első lépésként ajánlott a szimulációt validálni a táblázatban megadott értékekkel, amikor a vasmag a szolenoid közepében van. Majd ezt követően érdemes vizsgálni a két mennyiséget a vasmag pozíciójának függvényében. |
| − | |||
| − | === Geometria elkészítése SpaceClaim- | + | == Példa megoldása == |
| − | A | + | A következőkben a mágnesszelep megoldása és az eredmények kiértékelése kerül bemutatásra. |
| + | {| width=100% | ||
| + | |- | ||
| + | | align=center style="width: 48%;|'''[http://www.femm.info/wiki/HomePage Finite Elemenet Method Magnetics]''' | ||
| + | | align=center style="width: 4%; | | ||
| + | | align=center style="width: 48%; |'''[https://www.ansys.com/academic/free-student-products ANSYS Discovery AIM]''' | ||
| + | |- | ||
| + | | align=left style="width: 48%;|A FEMM szoftver használatához segítséget nyújt a következő két videó: | ||
| + | * [https://www.youtube.com/watch?v=RpqqISH_Gho&t=183s FEMM (Finite Element Method Magnetics) - Bevezető] | ||
| + | * [https://www.youtube.com/watch?v=jLkrtr9rlt4&t=102s FEMM és Scilab összekapcsolása]<br /> | ||
| + | <span style="color:white">"Nationalism is an infantile disease. It is the measles of mankind." [Albert Einstein]</span> | ||
| + | | align=center style="width: 4%; | | ||
| + | | align=left style="width: 48%; |A Discovery AIM szoftver használatához segítséget nyújt a következő három videó: | ||
| + | * [https://www.youtube.com/watch?v=-Lq_KK0Bevc Geometria elkészítése ANSYS SpaceClaim-el] | ||
| + | * [https://www.youtube.com/watch?v=CZ6ktjo1rCs&t=376s Feladat specifikálása ANSYS Discovery AIM segítségével] | ||
| + | * [https://www.youtube.com/watch?v=Rikdd39TSmE Ez eredmények kiértékelése / Paraméterezés.] | ||
| + | |- | ||
| + | | align=left style="width: 48%;|A FEMM kétdimenziós feladatok (síkbeli vagy hengerszimmetrikus) megoldására alkalmas. A vizsgált példa hengerszimmetrikus mágneses feladat. Ezért a ''Create a new problem'' ablakban a ''Magnetics Problem'' feladattípust kell választani. Ezt követően érdemes elsőnek a ''Problem'' menüre kattintva megadni a feladat típusát (''Problem Type'' - ''Axisymmetric''), a hossz mértékegységét (''Length Units'' - ''Milimeters''). A többi paraméter maradhat az alapbeállítás, de például frekvenciatartománybeli (harmonikus) feladat esetében itt lehet specifikálni a gerjesztés frekvenciáját.<br /> | ||
| + | [[File:FEMM Geometria.PNG|180px|thumb|left|alt=Az üzemanyag befecskendező mágnesszelep geometriája FEMM-ben. |Az üzemanyag befecskendező mágnesszelep geometriája FEMM-ben.]] A geometria elkészítésénél először a pontokat, majd a különböző tartományokat határoló vonalakat kell definiálni. A pontok a kurzor segítségével is elhelyezhetők, azonban ennek pontossága függ a rácspont sűrűségétől. Ezért célszerűbb a tabulátort (Tab) használni, ahol pontosan megadható a pont két koordinátája. Jelen (hengerszimmetrikus) esetben az a két koordináta az ''r'' (vízszintes) és a ''z'' (függőleges) koordináta. Majd a pontok a kurzor segítségével összeköthetőek, miután az ''Operation/Node'' menüről átváltunk az ''Operation/Segment'' műveletre. Az ábrán látható elrendezést kell kapnunk, ami már tartalmazza a lezárást is (100mm x 50mm).<br /> A következő lépés az anyagok (''Properties/Materials'') és a feladatnál használt peremfeltétel (''Properties/Boundary'') definiálása. Ennél a példánál az anyagparaméternél adjuk meg a gerjesztést is mint áramsűrűség (''Source Current Density''). A <math>J</math> áramsűrűséget a következő összefüggésel tudjuk meghatározni: | ||
| + | ::<math>J=\frac{N\cdot I}{A}</math>, | ||
| + | ahol <math>N</math> a menetszám, <math>I</math> az egy menetre jutó áramerősség és <math>A</math> a tekercs keresztmetszete. A gerjesztés másik megadási módja a ''Properties/Circuits'' menünél definiálni a tekercset, majd megadni hozzá a menetszámot. Ebben az esetben a FEMM automatikusan számolja a tekercshez kapcsolódó paramétereket (pl. induktivitás, fluxuskapcsolódás). A peremfeltétel (''Properties/Boundary'') ennél a példánál a feladat megoldásához használt <math>\vec{A}</math> mágneses vektorpotenciál közvetlen előírása (''Prescribed A'') a peremen (Dirichlet vagy elsőfajú). A vektorpotenciál értéke nulla a peremen, ami annyit jelent, hogy a <math>\vec{B}</math> mágneses fluxussűrűségnek csak tangenciális irányú komponense van.<br /> Ha definiáltuk az anyagokat és a peremfeltételt az ''Operation/Block'' menüre váltva megadjuk a feladat tartományait. Majd a tartományok (''Block'') vagy peremek (''Segment'') jobb egérgombbal történő kijelölése utána a Space lenyomásával tudjuk definiálni a tartományhoz / peremhez tartozó anyagot / peremfeltételt.<br /> Ha mindezzel megvagyunk mentsük el a feladatot. | ||
| − | + | A feladat elkészítése után a diszkretizálás következik. A hálót a ''Mesh/Create Mesh'' menü segítségével tudjuk elkészíteni. A FEMM-ben is van lehetőség a tartományra/peremre megadni a végeselem méretét, de ebben az esetben megfelelő lesz az alapháló. A hálózást követően az ''Analyzis/Analyse'' menüvel tudjuk elindítani a megoldót.<br /> | |
| + | Az eredményeket a ''Analyzis/View Results'' menü segítségével tudjuk megjeleníteni. Az alábbi két ábra egy-egy példa a FEMM-ben elérhető lehetőségekre.<br />[[File:FEMM Bfield.png|260px|thumb|left|alt=Az üzemanyag befecskendező mágnesszelep geometriája FEMM-ben. |A mágneses fluxussűrűség és az ekvipotenciális vonalak a mágnesszelepben.]] [[File:FEMM Hfield.png|288px|thumb|right|alt=Az üzemanyag befecskendező mágnesszelep geometriája FEMM-ben. |A mágneses fluxussűrűség vektorok és a mágneses térerősség eloaszlása.]]<br />Az utófeldolgozásnál van lehetőség a vizsgált feladatnál kiszámolni különböző mennyiségeket. Ennél a feladatnál a vasmagra ható erő és a tekercs induktivitása a két számítandó mennyiség.<br />A gerjesztést az anyagparamétereknél definiáltuk, ezért nem számolja a FEMM az induktivitást. Az induktivitás meghatározására a végeselem-módszer esetében legelterjedtebben alkalmazott módszer a mágneses energiából történő meghatározás, mert az könnyen számítható. A mágneses energiából az <math>L</math> induktivitást a következő képlettel lehet meghatározni: | ||
| + | ::<math>L=\frac{2\cdot W_{\text{m}}}{I^2}</math>, | ||
| + | ahol <math>W_{\text{m}}</math> a teljes rendszer mágneses energiája, <math>I</math> a gerjesztőáram. Az induktivitás meghatározásához először meghatározzuk a mágneses energiát (''Magnetic field energy''), amit a FEMM segítségével számolunk. Ehhez az összes tartományt kijelöljük, majd az integrálás (''Integrate'' menü) ablakban kiválasztjuk a mágneses energiát. Az így kapott értéket behelyettesítve kapjuk az tekercs induktivitását a vasmag adott pozíciójában.<br />A vasmagra ható erőt felületi és görbére vett integrálás segítségével is meghatározható. Felületi integrálás esetében azt a tartományt (vasmag) kell kijelölni, ahol szeretném az erőt meghatározni. Azonban az integrálásnál mindkét esetben a Maxwell-féle feszültségtenzorral (''Force via Weighted Stress Tensor'') kell számolni. | ||
| + | | align=center style="width: 4%; | | ||
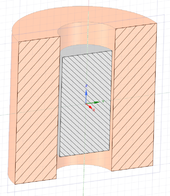
| + | | align=left style="width: 48%; |[[File:Pelda_Geometry_CrossSection.png|170px|thumb|left|alt=Az üzemanyag befecskendező mágnesszelep geometriájának keresztmetszete. |Az üzemanyag befecskendező mágnesszelep geometriájának keresztmetszete.]] Az ANSYS Discovery AIM (''ANSYS Integrated Multiphysics'') szoftverben elektromágneses szempontból. az alapbeállításokat használva sztatikus mágneses, elektrosztatika és frekvenciatartománybeli feladatokat lehet vizsgálni. Elsősorban a tervezőknek ajánlja az ANSYS, a koncepció fázisban lévő fejlesztéseknél egy-egy gyors ellenőrzéshez. De ettől függetlenül jól alkalmazható a lehetőségeinek megfelelően tetszőleges feladat megoldására is (''ahogy ezt későbbi feladatoknál látjuk majd'').<br />A Discovery AIM-nél a geometria elkészítéséhez a SpaceClaim áll rendelkezésre vagy egy CAD szoftverben elkészített geometria importálására van lehetőség. | ||
| − | + | A feladat geometriájának elkészítése itt nem kerül részletezésre, csak a gerjesztéshez későbbi megadásához szükséges lépések, amelyek nem egyérteműek, kerülnek részletezésre. Azt azonban fontos megjegyezni, hogy a SpaceClaim tudja kezelni az ékezetes betűket (magyar ABC), de a Discovery AIM nem. Tehát fontos ügyelni arra, hogy csak az angol ABC betűi szerepeljenek az elnevezésekben. | |
| − | + | Háromdimenziós esetben a tekercs egy keresztmetszetére írom elő a gerjesztést. Ehhez először egy síkor hozunk létre a tekercs-vasmag elrendezés keresztmetszetében a ''Design - Plane'' ikon segítségével. Ezt követően a baloldalon található ''Szerkezet'' (''Structure'') ablakban a ''Tervkomponensre'' (struktúra fa gyökérébe) kattintva hozzáadunk egy ''új komponenst'' (''New Component''). Az új komponens tulajdonságai között (új komponensre kattintva Tulajdonságok (Properties)) a ''Topológia megosztása'' (''Shared Topology'') legyen ''Megosztásra'' (''Shared'') állítva. Ha ezt megtettük, a tekercset húzzuk bele (drag and drop) az új komponensbe. Majd a következő lépésként rajzoljuk meg a tekercs keresztmetszetét felhasználva az elrendezés metszeti nézetét. Ha megrajzoltuk a tekercs keresztmetszetét, annak is az új komponens fájában kell lennie. Ennek köszönhetően az ANSYS Discovery AIM a megrajzolt felületet a tekercs keresztmetszeteként fogja kezelni, így erre a felületre előírható a gerjesztés. Végül a ''Tervkomponensre'' kattintva jobbegérgombbal válasszuk ki az ''Aktív komponens'' (''Active Component'') lehetőséget, hogy a teljes geometria aktív legyen, ne csak az újonnan létrehozott komponens. Valamint itt lehet paraméterezni a geometria méreteit és egymáshoz képesti helyzetét, tehát például a vasmag mozgásának figyelembevételét. | |
| − | + | Az ANSYS Discovery AIM elindítását követően válasszuk az ''Electromagnetics'' lehetőséget. Ezt követően a szoftver végigvezet minket a teljes szimuláción, emiatt minden lépés nem kerül részletezésre. | |
| − | Az | ||
| − | A | + | A geometria importálását követően a feladat típusa ''Electromagnetic'', a forrás ''Applied current'' és ''DC''. A feladat termikus viselkedése ''Constant temperature'' és opcióként válasszuk ki az erő (''Compute force'') és induktivitás (''Compute inductance'') számítást. Majd legvégül válasszuk a ''Create surround automatically'' opciót. Ez a lehetőség akkor fontos, ha a méretek vagy pozíció változni fog a szimuláció során. |
| − | + | Az első beállításokat követően az anyagokat kell definiálni az egyes tartományokra. Háromdimenziós feladatnál fontos, hogy térfogatokra (''Volume'') definiáljuk az anyagtulajdonságokat. Majd a ''Finish'' gombra kattintva létrehozzuk a feladatot. Azonban a ''Physics'' beállításainál még definiálni kell hol számoljuk az erőt és a gerjesztés megadása is hiányzik. Az erő számításánál a vasmagot kell kijelölni, a számítási mód a ''Virtual'' ([https://hu.wikipedia.org/wiki/A_virtu%C3%A1lis_munka_elve Virtuális munka elve]). Majd ezt követően a gerjesztés kell definiálni a tekercsbe berajzolt keresztmetszetre. Itt az áramerősséget és a menetszámot kell megadni, amiből a szoftver a FEMM-nél található képlet alapján az áramsűrűséget meghatározza. A keresztmetszet kiválasztásához javasolt a lezárás és a tekercs elrejtése (''Hide Body''). | |
| − | Ha | + | Ha ezekkel készen vagyunk és mindent (megfelelően) definiáltunk, akkor a piros mező felkiáltójellel átvált sárga mezőre, benne egy fekete villámmal. Már csak a megoldás van hátra (''Solve Physics''). A megoldó beállításai maradhatnak az alapbeállításon, illetve a diszkretizálással se kell törődni, mert a megoldó adaptívan finomítja a felbontást. |
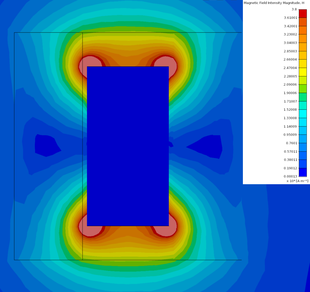
| − | + | A megoldást követően az eredményt (''Results'') is frissíteni kell. Ekkor történik meg az AIM-ben alapbeállításként definiált ábrákhoz a térváltozók és az általunk beállított mennyiségek kiszámítása. Tehát ebben az esetben az erő vagy az induktivitás meghatározása automatikusan történik az előzetes beállítások alapján. A különböző térváltozók tetszőleges felületre, térfogatra vagy előre definiált keresztmetszetre kirajzoltathatóak, ahogy a lenti két kép is mutatja. Az ábrák a mágnesszelep középében mutatják a térváltozókat, így összehasonlítható a FEMM-nél kapott eredményekkel. | |
| − | A | + | [[File:DiscoveryAIM_Bfield.png|230px|thumb|left|alt=Az üzemanyag befecskendező mágnesszelep geometriája FEMM-ben. |A mágneses fluxussűrűség a mágnesszelepben.]] [[File:DiscoveryAIM_Hfield.png|310px|thumb|right|alt=Az üzemanyag befecskendező mágnesszelep geometriája FEMM-ben. |A mágneses fluxussűrűség vektorok és a mágneses térerősség eloaszlása.]]<br /> |
| + | <span style="color:white">"Nationalism is an infantile disease. It is the measles of mankind." [Albert Einstein]</span> | ||
| + | |- | ||
| + | | align=center style="width: 48%;| | ||
| + | {| class="wikitable" align=center style="text-align: center; width: 400px; height: 100px;" | ||
| + | |+ A szimulációval kapott eredmények. | ||
| + | ! Szoftver | ||
| + | ! Maxwell 2D | ||
| + | ! FEMM | ||
| + | |- | ||
| + | ! Induktivitás [<math>\text{mH}</math>] | ||
| + | | 51,911 || 51,821 | ||
| + | |- | ||
| + | ! Erő [<math>\mu\text{N}</math>] | ||
| + | | 88,603 | ||
| + | | 74,53 | ||
| + | |} | ||
| + | | align=center style="width: 4%; | | ||
| + | | align=center style="width: 48%; | | ||
| + | {| class="wikitable" align=center style="text-align: center; width: 400px; height: 100px;" | ||
| + | |+ A szimulációval kapott eredmények. | ||
| + | ! Szoftver | ||
| + | ! Maxwell 3D | ||
| + | ! Discovery AIM | ||
| + | |- | ||
| + | ! Induktivitás [<math>\text{mH}</math>] | ||
| + | | 51,812 || 51,985 | ||
| + | |- | ||
| + | ! Erő [<math>\mu\text{N}</math>] | ||
| + | | 63,29 | ||
| + | | 45,037 | ||
| + | |} | ||
| + | |- | ||
| + | | align=left style="width: 48%;| | ||
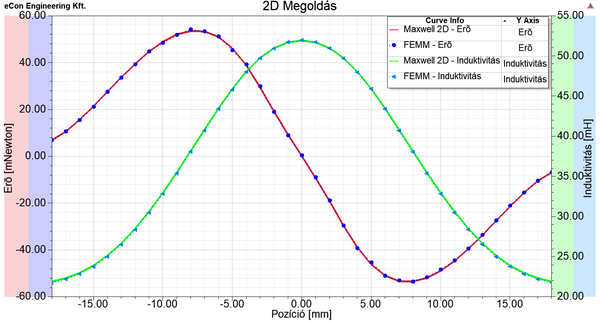
| + | A FEMM esetében hosszú és fáradságos mindig újrarajzolni a geometriát, ahhoz, hogy vizsgálható legyen a két számolt mennyiségek a vasmag pozíciójának függvényében ('''De természetesen kézzel, egyesével is megoldható.'''). Ehelyett célszerűbb ezt egy szkript ([https://www.lua.org/ ''Lua''] - ez a FEMM beépített programozási nyelve; [https://www.scilab.org/ ''Scilab'']; [https://www.gnu.org/software/octave/ ''GNU Octave''] - ezek szabadon hozzáférhetőek) segítségével megoldani. Az eredeti feladaton annyit kell ehhez módosítani, hogy a Vasmag mint tartomány és annak vonalai, pontjai egy csoportban (''In Group'') legyenek. Majd ez a csoport már egyszerre kijelölhető a ''mi_selectgroup(csoport száma)'' paranccsal és az ''mi_movetranslate(dr,dz)'' paranccsal elmozgatható egy újabb pozícióba. A vasmag elmozgatásából kapott eredményeket a lenti kép mutatja. Az erőnek a ''z''-irányú komponensét ábrázoltuk, ami előjelet is vált a két végállapot között. Az induktivitásnak pedig a vasmag 0 mm pozícióban van maximuma, mert akkor a legkisebb a mágneses ellenállása (reluktanciája) a rendszernek. | ||
| + | | align=center style="width: 4%; | | ||
| + | | align=left style="width: 48%; | A Discovery AIM esetében is van lehetőség szkript írására, de ennél jóval egyszerűbb a paramétervizsgálat. Ehhez a ''Geometry/Edit Geometry'' gombbal visszamegyünk a geometriához, ahol a ''Design/Move'' művelettel elmozgatjuk a kezdeti pozícióba a vasmagot, majd a mozgatás távolsága mellett megjelenő '''P''' betűre kattintva létrehozzuk a paramétert. Ezen paraméter átírásával tudjuk a vasmag helyzetét változtatni. A létrehozott változót a baloldali oszlop ''Group'' fülén találjuk, ahol átnevezhetjük, hogy a későbbiekben könnyebben azonosíthassuk. Majd az AIM-en belül, az erő és induktivitás értékét szintén paraméterezni kell. Ha ezekkel megvagyunk a ''Study Physics'' nézetről átváltunk a ''Project'' nézetre. Itt található a ''Parameter Sets'', amire kétszer kattintva megnyílik. Itt van lehetőség újabb pozíciók definiálására, amiket az ''Update All Design Points'' gombra kattintva kiszámol nekünk a szoftver. A paramétervizsgálat eredményét a lenti ábra mutatja. Háromdimenziós esetben a vasmagra ható erő hosszát ábrázoltam, ezért csak pozitív értékeket vesz fel. | ||
| + | |- | ||
| + | | align=center style="width: 48%;| | ||
| + | [[File:Pelda1 2D Megoldas.png|600px|thumb|left|alt=A kétdimenziós szimulációval kapott eredmények összehasonlítása.|A kétdimenziós szimulációval kapott eredmények összehasonlítása.]] | ||
| + | | align=center style="width: 4%; | | ||
| + | | align=center style="width: 48%; | | ||
| + | [[File:Pelda1 3D Megoldas.png|600px|thumb|left|alt=A háromdimenziós szimulációval kapott eredmények összehasonlítása.|A háromdimenziós szimulációval kapott eredmények összehasonlítása.]] | ||
| + | |} | ||
| − | == | + | == Irodalomjegyzék == |
{{reflist}} | {{reflist}} | ||
Latest revision as of 20:01, 28 January 2020
|
Üzemanyag befecskendező mágnesszelep | |
| Az üzemanyag befecskendező működés közben. [1] | Az üzemanyag befecskendezőnél a B vektorok a szolenoid bekapcsolását követően. |
|
| |
|
Oktató
|
További oktatók:
|
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása az üzemanyag befecskendező szolenoidjának szimulációján keresztül.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A sztatikus mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- A geometria elkészítéséhez CAD rendszer ismerete (háromdimenziós esetben).
A feladat
A vizsgált feladat (ha elhanyagoljuk a bekapcsoláskor fellépő átmeneti állapotot) állandósult állapotban sztatikus mágneses feladatnak tekinthető. A vasmag mozgásának (szelep nyitása / zárása) hatását is ennek megfelelően vizsgáljuk, vagyis minden pozícióhoz tartozik egy-egy szimuláció. Erre a különböző szoftverek más és más megoldást adnak (szkript, paramétervizsgálat). A mágnesszelep megoldása itt a FEMM és az ANSYS Discovery AIM Student szoftverekkel kerül bemutatásra, ezzel a féléves feladat elkészítéséhez is segítséget nyújtva.
A feladatban szereplő anyagok:
- Vasmag: Nemlineáris mágnesezési görbével rendelkező acél (Steel1008);
- Tekercs: Anyaga réz (Copper) és 2000 menetes (Number of Conductors). Az áramerősség (Current) 0,2 A;
- Lezárás: Levegő (Air).
A feladat a mágnesszelep induktivitásának és a vasmagra ható erőnek a meghatározása. Első lépésként ajánlott a szimulációt validálni a táblázatban megadott értékekkel, amikor a vasmag a szolenoid közepében van. Majd ezt követően érdemes vizsgálni a két mennyiséget a vasmag pozíciójának függvényében.
Példa megoldása
A következőkben a mágnesszelep megoldása és az eredmények kiértékelése kerül bemutatásra.
| Finite Elemenet Method Magnetics | ANSYS Discovery AIM | |||||||||||||||||||
| A FEMM szoftver használatához segítséget nyújt a következő két videó:
"Nationalism is an infantile disease. It is the measles of mankind." [Albert Einstein] |
A Discovery AIM szoftver használatához segítséget nyújt a következő három videó: | |||||||||||||||||||
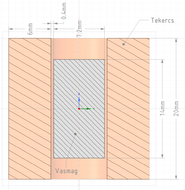
| A FEMM kétdimenziós feladatok (síkbeli vagy hengerszimmetrikus) megoldására alkalmas. A vizsgált példa hengerszimmetrikus mágneses feladat. Ezért a Create a new problem ablakban a Magnetics Problem feladattípust kell választani. Ezt követően érdemes elsőnek a Problem menüre kattintva megadni a feladat típusát (Problem Type - Axisymmetric), a hossz mértékegységét (Length Units - Milimeters). A többi paraméter maradhat az alapbeállítás, de például frekvenciatartománybeli (harmonikus) feladat esetében itt lehet specifikálni a gerjesztés frekvenciáját. A geometria elkészítésénél először a pontokat, majd a különböző tartományokat határoló vonalakat kell definiálni. A pontok a kurzor segítségével is elhelyezhetők, azonban ennek pontossága függ a rácspont sűrűségétől. Ezért célszerűbb a tabulátort (Tab) használni, ahol pontosan megadható a pont két koordinátája. Jelen (hengerszimmetrikus) esetben az a két koordináta az r (vízszintes) és a z (függőleges) koordináta. Majd a pontok a kurzor segítségével összeköthetőek, miután az Operation/Node menüről átváltunk az Operation/Segment műveletre. Az ábrán látható elrendezést kell kapnunk, ami már tartalmazza a lezárást is (100mm x 50mm). A következő lépés az anyagok (Properties/Materials) és a feladatnál használt peremfeltétel (Properties/Boundary) definiálása. Ennél a példánál az anyagparaméternél adjuk meg a gerjesztést is mint áramsűrűség (Source Current Density). A [math]J[/math] áramsűrűséget a következő összefüggésel tudjuk meghatározni:
ahol [math]N[/math] a menetszám, [math]I[/math] az egy menetre jutó áramerősség és [math]A[/math] a tekercs keresztmetszete. A gerjesztés másik megadási módja a Properties/Circuits menünél definiálni a tekercset, majd megadni hozzá a menetszámot. Ebben az esetben a FEMM automatikusan számolja a tekercshez kapcsolódó paramétereket (pl. induktivitás, fluxuskapcsolódás). A peremfeltétel (Properties/Boundary) ennél a példánál a feladat megoldásához használt [math]\vec{A}[/math] mágneses vektorpotenciál közvetlen előírása (Prescribed A) a peremen (Dirichlet vagy elsőfajú). A vektorpotenciál értéke nulla a peremen, ami annyit jelent, hogy a [math]\vec{B}[/math] mágneses fluxussűrűségnek csak tangenciális irányú komponense van. A feladat elkészítése után a diszkretizálás következik. A hálót a Mesh/Create Mesh menü segítségével tudjuk elkészíteni. A FEMM-ben is van lehetőség a tartományra/peremre megadni a végeselem méretét, de ebben az esetben megfelelő lesz az alapháló. A hálózást követően az Analyzis/Analyse menüvel tudjuk elindítani a megoldót. Az utófeldolgozásnál van lehetőség a vizsgált feladatnál kiszámolni különböző mennyiségeket. Ennél a feladatnál a vasmagra ható erő és a tekercs induktivitása a két számítandó mennyiség. A gerjesztést az anyagparamétereknél definiáltuk, ezért nem számolja a FEMM az induktivitást. Az induktivitás meghatározására a végeselem-módszer esetében legelterjedtebben alkalmazott módszer a mágneses energiából történő meghatározás, mert az könnyen számítható. A mágneses energiából az [math]L[/math] induktivitást a következő képlettel lehet meghatározni:
ahol [math]W_{\text{m}}[/math] a teljes rendszer mágneses energiája, [math]I[/math] a gerjesztőáram. Az induktivitás meghatározásához először meghatározzuk a mágneses energiát (Magnetic field energy), amit a FEMM segítségével számolunk. Ehhez az összes tartományt kijelöljük, majd az integrálás (Integrate menü) ablakban kiválasztjuk a mágneses energiát. Az így kapott értéket behelyettesítve kapjuk az tekercs induktivitását a vasmag adott pozíciójában. |
Az ANSYS Discovery AIM (ANSYS Integrated Multiphysics) szoftverben elektromágneses szempontból. az alapbeállításokat használva sztatikus mágneses, elektrosztatika és frekvenciatartománybeli feladatokat lehet vizsgálni. Elsősorban a tervezőknek ajánlja az ANSYS, a koncepció fázisban lévő fejlesztéseknél egy-egy gyors ellenőrzéshez. De ettől függetlenül jól alkalmazható a lehetőségeinek megfelelően tetszőleges feladat megoldására is (ahogy ezt későbbi feladatoknál látjuk majd). A Discovery AIM-nél a geometria elkészítéséhez a SpaceClaim áll rendelkezésre vagy egy CAD szoftverben elkészített geometria importálására van lehetőség. A feladat geometriájának elkészítése itt nem kerül részletezésre, csak a gerjesztéshez későbbi megadásához szükséges lépések, amelyek nem egyérteműek, kerülnek részletezésre. Azt azonban fontos megjegyezni, hogy a SpaceClaim tudja kezelni az ékezetes betűket (magyar ABC), de a Discovery AIM nem. Tehát fontos ügyelni arra, hogy csak az angol ABC betűi szerepeljenek az elnevezésekben. Háromdimenziós esetben a tekercs egy keresztmetszetére írom elő a gerjesztést. Ehhez először egy síkor hozunk létre a tekercs-vasmag elrendezés keresztmetszetében a Design - Plane ikon segítségével. Ezt követően a baloldalon található Szerkezet (Structure) ablakban a Tervkomponensre (struktúra fa gyökérébe) kattintva hozzáadunk egy új komponenst (New Component). Az új komponens tulajdonságai között (új komponensre kattintva Tulajdonságok (Properties)) a Topológia megosztása (Shared Topology) legyen Megosztásra (Shared) állítva. Ha ezt megtettük, a tekercset húzzuk bele (drag and drop) az új komponensbe. Majd a következő lépésként rajzoljuk meg a tekercs keresztmetszetét felhasználva az elrendezés metszeti nézetét. Ha megrajzoltuk a tekercs keresztmetszetét, annak is az új komponens fájában kell lennie. Ennek köszönhetően az ANSYS Discovery AIM a megrajzolt felületet a tekercs keresztmetszeteként fogja kezelni, így erre a felületre előírható a gerjesztés. Végül a Tervkomponensre kattintva jobbegérgombbal válasszuk ki az Aktív komponens (Active Component) lehetőséget, hogy a teljes geometria aktív legyen, ne csak az újonnan létrehozott komponens. Valamint itt lehet paraméterezni a geometria méreteit és egymáshoz képesti helyzetét, tehát például a vasmag mozgásának figyelembevételét. Az ANSYS Discovery AIM elindítását követően válasszuk az Electromagnetics lehetőséget. Ezt követően a szoftver végigvezet minket a teljes szimuláción, emiatt minden lépés nem kerül részletezésre. A geometria importálását követően a feladat típusa Electromagnetic, a forrás Applied current és DC. A feladat termikus viselkedése Constant temperature és opcióként válasszuk ki az erő (Compute force) és induktivitás (Compute inductance) számítást. Majd legvégül válasszuk a Create surround automatically opciót. Ez a lehetőség akkor fontos, ha a méretek vagy pozíció változni fog a szimuláció során. Az első beállításokat követően az anyagokat kell definiálni az egyes tartományokra. Háromdimenziós feladatnál fontos, hogy térfogatokra (Volume) definiáljuk az anyagtulajdonságokat. Majd a Finish gombra kattintva létrehozzuk a feladatot. Azonban a Physics beállításainál még definiálni kell hol számoljuk az erőt és a gerjesztés megadása is hiányzik. Az erő számításánál a vasmagot kell kijelölni, a számítási mód a Virtual (Virtuális munka elve). Majd ezt követően a gerjesztés kell definiálni a tekercsbe berajzolt keresztmetszetre. Itt az áramerősséget és a menetszámot kell megadni, amiből a szoftver a FEMM-nél található képlet alapján az áramsűrűséget meghatározza. A keresztmetszet kiválasztásához javasolt a lezárás és a tekercs elrejtése (Hide Body). Ha ezekkel készen vagyunk és mindent (megfelelően) definiáltunk, akkor a piros mező felkiáltójellel átvált sárga mezőre, benne egy fekete villámmal. Már csak a megoldás van hátra (Solve Physics). A megoldó beállításai maradhatnak az alapbeállításon, illetve a diszkretizálással se kell törődni, mert a megoldó adaptívan finomítja a felbontást. A megoldást követően az eredményt (Results) is frissíteni kell. Ekkor történik meg az AIM-ben alapbeállításként definiált ábrákhoz a térváltozók és az általunk beállított mennyiségek kiszámítása. Tehát ebben az esetben az erő vagy az induktivitás meghatározása automatikusan történik az előzetes beállítások alapján. A különböző térváltozók tetszőleges felületre, térfogatra vagy előre definiált keresztmetszetre kirajzoltathatóak, ahogy a lenti két kép is mutatja. Az ábrák a mágnesszelep középében mutatják a térváltozókat, így összehasonlítható a FEMM-nél kapott eredményekkel. "Nationalism is an infantile disease. It is the measles of mankind." [Albert Einstein] | |||||||||||||||||||
|
| |||||||||||||||||||
|
A FEMM esetében hosszú és fáradságos mindig újrarajzolni a geometriát, ahhoz, hogy vizsgálható legyen a két számolt mennyiségek a vasmag pozíciójának függvényében (De természetesen kézzel, egyesével is megoldható.). Ehelyett célszerűbb ezt egy szkript (Lua - ez a FEMM beépített programozási nyelve; Scilab; GNU Octave - ezek szabadon hozzáférhetőek) segítségével megoldani. Az eredeti feladaton annyit kell ehhez módosítani, hogy a Vasmag mint tartomány és annak vonalai, pontjai egy csoportban (In Group) legyenek. Majd ez a csoport már egyszerre kijelölhető a mi_selectgroup(csoport száma) paranccsal és az mi_movetranslate(dr,dz) paranccsal elmozgatható egy újabb pozícióba. A vasmag elmozgatásából kapott eredményeket a lenti kép mutatja. Az erőnek a z-irányú komponensét ábrázoltuk, ami előjelet is vált a két végállapot között. Az induktivitásnak pedig a vasmag 0 mm pozícióban van maximuma, mert akkor a legkisebb a mágneses ellenállása (reluktanciája) a rendszernek. |
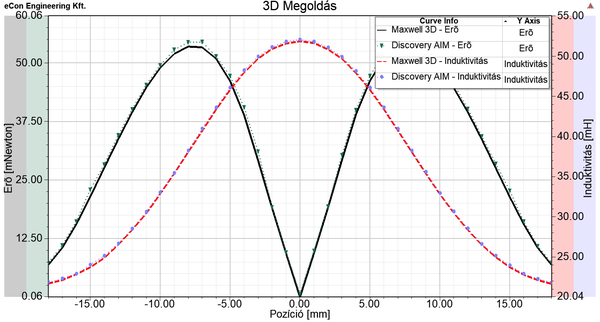
A Discovery AIM esetében is van lehetőség szkript írására, de ennél jóval egyszerűbb a paramétervizsgálat. Ehhez a Geometry/Edit Geometry gombbal visszamegyünk a geometriához, ahol a Design/Move művelettel elmozgatjuk a kezdeti pozícióba a vasmagot, majd a mozgatás távolsága mellett megjelenő P betűre kattintva létrehozzuk a paramétert. Ezen paraméter átírásával tudjuk a vasmag helyzetét változtatni. A létrehozott változót a baloldali oszlop Group fülén találjuk, ahol átnevezhetjük, hogy a későbbiekben könnyebben azonosíthassuk. Majd az AIM-en belül, az erő és induktivitás értékét szintén paraméterezni kell. Ha ezekkel megvagyunk a Study Physics nézetről átváltunk a Project nézetre. Itt található a Parameter Sets, amire kétszer kattintva megnyílik. Itt van lehetőség újabb pozíciók definiálására, amiket az Update All Design Points gombra kattintva kiszámol nekünk a szoftver. A paramétervizsgálat eredményét a lenti ábra mutatja. Háromdimenziós esetben a vasmagra ható erő hosszát ábrázoltam, ezért csak pozitív értékeket vesz fel. | |||||||||||||||||||