Difference between revisions of "Lecture 1. - Assignment"

From Maxwell
Jump to: navigation, search
(→‎Evaluation of Results)
(→‎Knowledge needed to solve the problem)
 
(64 intermediate revisions by the same user not shown)
Line 9: Line 9:
 
[[File:Pelda ResultsB.png|550px]]
 
[[File:Pelda ResultsB.png|550px]]
 
|-
 
|-
−
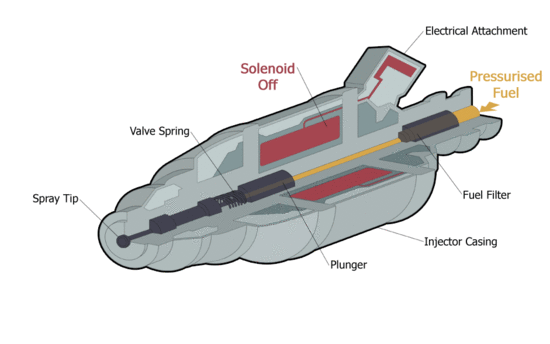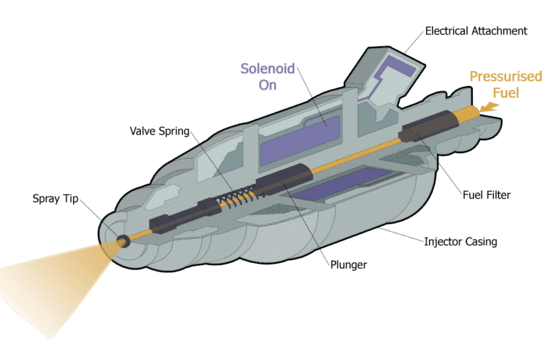
|align=center | The fuel injection in operation. <ref>https://upload.wikimedia.org/wikipedia/commons/2/29/Injector3.gif</ref>
+
|align=center | <span style="font-size:88%;">'''The fuel injection in operation.'''</span> <ref>https://upload.wikimedia.org/wikipedia/commons/2/29/Injector3.gif</ref>
−
|align=center | The magnetic flux density vectors in the plunger after switch on the solenoid.
+
|align=center | <span style="font-size:88%;">'''The magnetic flux density vectors in the plunger after switch on the solenoid.'''</span>
 
|- valign=top
 
|- valign=top
 
| width=50% |
 
| width=50% |
 
'''Instructor'''
 
'''Instructor'''
−
* Dániel Marcsa (lecturer)
+
* [http://wiki.maxwell.sze.hu/index.php/Marcsa Dániel Marcsa] (lecturer)
 
* Lectures: Monday, 14:50 - 16:25 (D201), 16:30 - 17:15 (D105)
 
* Lectures: Monday, 14:50 - 16:25 (D201), 16:30 - 17:15 (D105)
 
* Office hours: by request
 
* Office hours: by request
Line 22: Line 22:
 
* Office hours: -.
 
* Office hours: -.
 
|}
 
|}
−
 
+
<blockquote>
 
=== Purpose of the Assignment ===
 
=== Purpose of the Assignment ===
−
The student will learn the main steps of the finite element method, such as creating the model (creating or importing geometry), specifying material parameters, boundary conditions, and excitation through simulation of the electromagnetic part of fuel injector.
+
The student will learn the main steps of the finite element method, such as creating the model (creating or importing geometry), specifying material parameters, boundary conditions, and excitation through simulation of the electromagnetic part of the fuel injector.
  
 
=== Knowledge needed to solve the problem ===
 
=== Knowledge needed to solve the problem ===
 
* The steps of the finite element method;
 
* The steps of the finite element method;
−
* Theoretical knowledge of static magnetic field (for defining materials, for excitation);
+
* Theoretical knowledge of the static magnetic field (for defining materials, for excitation);
−
* Knowledge of CAD system to create geometry.
+
* Knowledge of the basics of [http://www.femm.info/wiki/HomePage FEMM] and [http://www.agros2d.org/ Agros2D].
−
 
 
−
=== Steps to solve the problem ===
 
−
After starting ANSYS AIM, select Electromagnetics by clicking on the ''Start'' button. Unlike the steps below, the task can be accomplished. When you use AIM, the messages that appear during the various steps help you in the simulation.
 
−
 
 
−
== Creating Geometry ==
 
−
The geometry of the problem can be made in ''[http://www.spaceclaim.com/en/default.aspx SpaceClaim]'', but also create another CAD software (AutoCAD; SolidWorks; Solid Edge; Catia; Creo; ...). The geometry consists of three parts, the iron core (''plunger''), the coil, and the cross-section of the coil for excitation.
 
  
−
The height of cylindrical core is 14mm and the radii is 3.6mm.
+
YouTube channel for [https://www.youtube.com/channel/UC7WzdNsW6Si-8e96mSluPPg Agros2D].<br/>
−
Dimensions of the coil: height is 20mm, innner radii is 4mm and outer radii is 10mm.
+
There are also a lot of videos on YouTube for using FEMM. For example [https://www.youtube.com/watch?v=1BKCkvr83j4 FEMM Tutorial]
  
−
=== Creating Geometry in SpaceClaim ===
+
== The Problem ==
−
[[File:Pelda_Geometry_CrossSection.png|285px|thumb|left|alt=Cross section of the fuel injector solenoid geometry. |Cross section of the fuel injector solenoid geometry.]]
 
−
To use SpaceClaim properly, the Help menu and videos on YouTube are a great help. Here I will only detail the creation of coil cross section. The presentation and the related practice will present the complete workflow.
 
  
−
First we create a plain in the cross-section of the coil core using the Design - Plane button. Then, in the ''Structure'' window, we add a ''New Component'' by clicking on ''Design Component''. In the properties of the new component, set ''Shared Topology'' to ''Share'' and we drag and drop the coil into the new component. Then, as the next step, draw the cross section of the coil using the cross-section plane of the arrangement. If you have drawn the cross section of the coil, it should also be in the tree of the new component. Because of the last step, the ANSYS Discovery AIM will treat the drawn surface as a cross-section of the coil, so this surface will use for excitation. Finally, right mouse button (RMB) clicking on ''Design Component'', and click on ''Active Component'' to make the entire geometry active, not just the newly created component. Also, it is possible to parameterize the dimensions of the geometry and their relative position, such as taking into account the movement of the iron core.
+
[[File:Problem01_Definition_CrossSection.png|405px|thumb|left| |The cross-section view of the solenoid valve.]]
 +
The problem (if we neglect the transient state occurring at the switch on) can be considered as an axisymmetric static magnetic problem. The effect of the movement of the iron core (valve opening/closing) is also examined accordingly, i.e. each position is an individual simulation.
  
−
If we created the geometry, save it, close SpaceClaim and start ANSYS Discovery AIM, and then select 'Electromagnetics'. Afterwards, Discovery AIM guide us through the complete simulation, so all the steps of the simulation are not detailed.
+
The height of the cylindrical core is 14mm and the radii is 3.6mm.
 +
Dimensions of the coil: height is 20mm, inner radii is 4mm and outer radii is 10mm.
  
−
After importing the geometry, the task type is ''Electromagnetic'', the source is ''Applied current'' and ''DC''. The thermal behavior of the task is ''Constant temperature'' and select 'Compute force' and 'Compute inductance' as an option. Finally, select 'Create surround automatically'. This option is important if the dimensions or position will change during the simulation.
+
'''The materials:'''
 +
* '''Core/Vasmag:''' ''Steel'' with nonlinear B-H curve ([https://drive.google.com/open?id=1hNmLPbkWXmyxgudRVMNpHXozw-OwUGly Steel1008]);
 +
* '''Coil/Tekercs:''' ''Copper'' (<math>\mu_r = 1.0</math>) and the ''number of turns'' is 2000. The ''current'' is 0.2 A;
 +
* '''Region:''' ''Air'' (<math>\mu_r = 1.0</math>).
  
−
== Defining the Materials, Excitation ==
+
The task is to determine the inductance of the solenoid valve and the force acting on the iron core. As a first step, it is recommended to validate the simulation with the values given in the table when the iron core is in the middle of the solenoid. Then it is worth examining the two quantities as a function of the position of the iron core.
−
We can define the materials by selecting the volumes.
 
  
−
The coil is made of copper (''Copper''), the core is steel 1008 (''Steel 1008''). If you want to modify some of their properties (conductivity, curve B-H), you can do it later in the properties of the materials.
+
=== Inductance Calculation ===
 +
The most widely used method for determining inductance in finite element analysis is based on magnetic energy. From the magnetic energy, the inductance <math>L</math> can be determined by the following formula:
 +
::<math>L=\frac{2\cdot W_{\text{m}}}{I^2}</math>
 +
where <math>W_{\text{m}}</math> the magnetic energy of the whole problem and <math>I</math> is the current (in this case 0.2A).
  
−
To define the excitation, the cross-section of the coil should be selected with a drawn surface, then the current (0.2A) and the number of turns (2000) should be specified. Here you can also define the fill factor for the coil.
+
=== Force Calculation ===
−
 
+
The force acting on the iron core can also be determined by surface and line integration. In the case of surface integration, the core should be selected. However, in both cases, Maxwell's stress tensor (''FEMM'' - Force via Weighted Stress Tensor / ''Agros2D'' - Maxwell force - y) used for integration.
−
After that, we do not take care of discretization and the settings of the solver. The basic settings will be appropriate. Adaptive meshing uses in the solution, so we do not deal with the discreatization for this problem.
 
  
 
== Evaluation of Results ==
 
== Evaluation of Results ==
−
[[File:Pelda ResultsChart2.png|300px|thumb|left|alt=Coil inductance and plunger force in the function of plunger position. |Coil inductance and plunger force in the function of plunger position.]]
+
<blockquote>
 +
[[File:Pelda1 2D Megoldas.png|530px|thumb|left|alt=Coil inductance and plunger force in the function of plunger position. |Coil inductance and plunger force in the function of plunger position.]]
  
−
Here you can plot the field quatities in the volume or on the surface and checked the vallue of the inductance of the coil and the acting force on iron core. The following values were obtained for these quantities, the arrangement according to the cross-sectional view being 15 mm, and -15 mm displacement of plunger means the 0 mm position.
+
Here you can plot the field quantities (magnetic flux density, magnetic vector potential, etc.) and checked the value of the inductance of the coil and the acting force on the iron core. The following values were obtained for these quantities, the arrangement according to the cross-sectional view being 0 mm position.
  
−
{| class = "wikitable" style = "text-align: center; width: 400px; height: 100px;"
+
{| class="wikitable" align=center style="text-align: center; width: 550px; height: 100px;"
−
|+ Results of simulation.
+
|+ The results of the simulation for validation.
−
! Position
+
! Software
−
! 0 mm
+
! Maxwell 2D
−
! 15 mm
+
! Maxwell 3D
 +
! FEMM
 +
! Agros2D
 
|-
 
|-
−
! Inductance [mH]
+
! Inductance [<math>\text{mH}</math>]
−
| 23.97 || 52.07
+
| 51.911 || 51.812 || 51.821 || 51.89
 
|-
 
|-
−
! Force [mN]
+
! Force [<math>\mu\text{N}</math>]
−
| 22.132
+
| 88.603
−
| 9.7617
+
| 63.29
−
|}
+
| 74.53
 +
| 57.45
 +
|}  
 +
 
 +
In addition, it is possible to parameterize the geometry or most of the simulation parameters (position, size, current, number, ...) via script (''FEMM - LUA script'', ''Agro2D - Python''). The result of a parameterized simulation is shown in the figure where the parameter is the position of the iron core. As a result, the modification of the parameter and the evaluation of results are automatic.
 +
</blockquote>
  
−
In addition, it is possible to parameterize different variables (position, size, current, number, ...). The result of a parameterized simulation is shown in the figure where the parameter is the position of the iron core. As a result, the modification of the parameter and the evaluation of results are automatic.
+
=== Knowledge needed to solve the problem ===
 +
The problem solution with
 +
* [https://youtu.be/bRMxkaXJnwQ FEMM]
 +
* [https://youtu.be/uO-jPNcDfIM Agros2D]
  
 
== References ==
 
== References ==
−
{{}} Reflist
+
{{Reflist}}

Latest revision as of 09:59, 6 April 2021

Fuel Injection Solenoid

Injector3.gif

Pelda ResultsB.png

The fuel injection in operation. [1] The magnetic flux density vectors in the plunger after switch on the solenoid.

Instructor

  • Dániel Marcsa (lecturer)
  • Lectures: Monday, 14:50 - 16:25 (D201), 16:30 - 17:15 (D105)
  • Office hours: by request

Teaching Assistants:

  • -
  • Office hours: -.

Purpose of the Assignment

The student will learn the main steps of the finite element method, such as creating the model (creating or importing geometry), specifying material parameters, boundary conditions, and excitation through simulation of the electromagnetic part of the fuel injector.

Knowledge needed to solve the problem

  • The steps of the finite element method;
  • Theoretical knowledge of the static magnetic field (for defining materials, for excitation);
  • Knowledge of the basics of FEMM and Agros2D.

YouTube channel for Agros2D.
There are also a lot of videos on YouTube for using FEMM. For example FEMM Tutorial

The Problem

The cross-section view of the solenoid valve.

The problem (if we neglect the transient state occurring at the switch on) can be considered as an axisymmetric static magnetic problem. The effect of the movement of the iron core (valve opening/closing) is also examined accordingly, i.e. each position is an individual simulation.

The height of the cylindrical core is 14mm and the radii is 3.6mm. Dimensions of the coil: height is 20mm, inner radii is 4mm and outer radii is 10mm.

The materials:

  • Core/Vasmag: Steel with nonlinear B-H curve (Steel1008);
  • Coil/Tekercs: Copper ([math]\mu_r = 1.0[/math]) and the number of turns is 2000. The current is 0.2 A;
  • Region: Air ([math]\mu_r = 1.0[/math]).

The task is to determine the inductance of the solenoid valve and the force acting on the iron core. As a first step, it is recommended to validate the simulation with the values given in the table when the iron core is in the middle of the solenoid. Then it is worth examining the two quantities as a function of the position of the iron core.

Inductance Calculation

The most widely used method for determining inductance in finite element analysis is based on magnetic energy. From the magnetic energy, the inductance [math]L[/math] can be determined by the following formula:

[math]L=\frac{2\cdot W_{\text{m}}}{I^2}[/math]

where [math]W_{\text{m}}[/math] the magnetic energy of the whole problem and [math]I[/math] is the current (in this case 0.2A).

Force Calculation

The force acting on the iron core can also be determined by surface and line integration. In the case of surface integration, the core should be selected. However, in both cases, Maxwell's stress tensor (FEMM - Force via Weighted Stress Tensor / Agros2D - Maxwell force - y) used for integration.

Evaluation of Results

Coil inductance and plunger force in the function of plunger position.
Coil inductance and plunger force in the function of plunger position.

Here you can plot the field quantities (magnetic flux density, magnetic vector potential, etc.) and checked the value of the inductance of the coil and the acting force on the iron core. The following values were obtained for these quantities, the arrangement according to the cross-sectional view being 0 mm position.

The results of the simulation for validation.
Software Maxwell 2D Maxwell 3D FEMM Agros2D
Inductance [[math]\text{mH}[/math]] 51.911 51.812 51.821 51.89
Force [[math]\mu\text{N}[/math]] 88.603 63.29 74.53 57.45

In addition, it is possible to parameterize the geometry or most of the simulation parameters (position, size, current, number, ...) via script (FEMM - LUA script, Agro2D - Python). The result of a parameterized simulation is shown in the figure where the parameter is the position of the iron core. As a result, the modification of the parameter and the evaluation of results are automatic.

Knowledge needed to solve the problem

The problem solution with

References

  1. ↑ https://upload.wikimedia.org/wikipedia/commons/2/29/Injector3.gif
Retrieved from "http://wiki.maxwell.sze.hu/index.php?title=Lecture_1._-_Assignment&oldid=2636"