Difference between revisions of "Kapacitás számítása"

From Maxwell
Jump to: navigation, search
(Created page with "{| width=100% |- | colspan=2 align=center | <font color='blue' size='+2'>Négyszög keresztmetszetű csőtápvonal (Rectangular waveguide)</font> |- | style="width: 100px;" al...")
 
(→‎A feladat célja)
 
(129 intermediate revisions by the same user not shown)
Line 2: Line 2:
 
|-
 
|-
 
| colspan=2 align=center |
 
| colspan=2 align=center |
−
<font color='blue' size='+2'>Négyszög keresztmetszetű csőtápvonal (Rectangular waveguide)</font>
+
<font color='blue' size='+2'>Kételektródás elrendezés kapacitásának számítása</font>
 
|-
 
|-
 
| style="width: 100px;" align=center |
 
| style="width: 100px;" align=center |
−
[[File:Waveguides real.jpeg|300px]]
+
[[File:CapacitorCalculation Geometry.png|550px|thumb|center|upright=2.0|alt= A feladat végeselemhálója és a peremek elnevezése.|A feladat végeselemhálója és a peremek elnevezése.]]
 
| align=center |
 
| align=center |
−
[[File:Waveguide EField TE10.gif|550px]]
+
[[File:CapacitanceCalculation ScreenShot.png|630px|thumb|center|upright=2.0|alt= A feladat megoldása ONELAB (Gmsh + GetDP) segítségével.|A feladat megoldása ONELAB (Gmsh + GetDP) segítségével.]]
−
|-
 
−
|align=center | <span style="font-size:88%;">'''Négyszög keresztmetszetű csőtápvonal.'''</span>
 
−
|align=center | <span style="font-size:88%;">'''Az elektromos térerősség terjedése a csőtápvonalban.'''</span> <span style="font-size:80%; color:blue;">[Kattints a képre az animáció megtekintéséhez.]</span>
 
 
|- valign=top
 
|- valign=top
 
| width=50% |
 
| width=50% |
 
''' '''
 
''' '''
 +
|-
 +
| style="text-align: left; width: 36%;" |
 +
'''Oktató'''
 +
* [http://wiki.maxwell.sze.hu/index.php/Marcsa Marcsa Dániel] (óraadó)
 +
* Előadás: -
 +
* Fogadóóra: egyeztetés alapján
 +
| style="text-align: left; width: 36%;" |
 +
'''További oktatók:'''
 +
* -
 +
* Fogadóóra: -.
 
|}
 
|}
  
 
=== A feladat célja ===
 
=== A feladat célja ===
−
[[File:Waveguide Geometry.png|360px|thumb|right|alt=A feladat geometriája. | A feladat geometriája.]]
+
[[File:CapacitanceCalculation 3DGeometry.png|360px|thumb|right|alt=A feladat geometriája. | A feladat geometriája.]]
−
[[File:TE10 WallCurrent.png|360px|thumb|right|alt=A kialakuló faláramok a négyszögletes hullámvezetőben. | A kialakuló faláramok a négyszögletes hullámvezetőben.]]
+
[[File:CapacitanceCalculation CrossSection.png|360px|thumb|right|alt=A feladat keresztmetszete a méretekkel. | A feladat keresztmetszete a méretekkel.]]
 +
 
 +
A hallgató megismerje a végeselem-módszerhez kapcsolódó főbb lépéseket, mint a geometria elkészítése vagy importálása, anyagparaméterek, peremfeltételek és gerjesztés megadása, eredmények megjelenítése. Emellett pedig bemutasson a hallgatónak egy szabadon hozzáférhető szoftvert, ami nagyon jól használható disszertációk és kutatások során, köszönhetően felhasználóbarát grafikus felületének és tetszőlegesen konfigurálható megoldójának.
 +
 
 +
A feladat példája [https://www.hvt.bme.hu/munkatarsak/oktatok/30-gyimothy-szabolcs Dr. habil Gyimóthy Szabolcs egyetemi docens] [https://www.youtube.com/watch?v=0ejifIdnHAI&list=PL5xmmBARdxpp36lVw-yv9Uck0sTgZOgLS&index=9 Elektromágneses terek előadásából] származik. Az előadást ajánlom mindenkinek, aki betekintést szeretne kapni a végeselem-módszer elméleti hátterébe, hogy mi az, amit legtöbbször a szoftverek elrejtenek a felhasználó elől.
 +
 
 +
A példa az előadásban a [https://www.mathworks.com/products/pde.html Matlab PDE Toolbox] segítségével kerül megoldásra. Itt a szabadon hozzáférhető [http://onelab.info/ ONELAB] ([http://gmsh.info/ Gmsh] + [http://getdp.info/ GetDP]) és a kereskedelmi [https://www.ansys.com/products/electronics/ansys-maxwell ANSYS Maxwell] szoftverekkel lesz a megoldás bemutatva. Ezen utóbbi szoftver elsősorban az előadásban elhangzott adaptív hálósűrítés miatt.
  
−
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása egy négyszög keresztmetszetű csőtápvonal esetében. A szimuláció beállításai és eredményei elősegítsék a más tárgyakból tanult elméleti ismeretek elmélyülését.
+
A [http://onelab.info/ ONELAB] a neve alapján (Open Numerical Engineering LABoratory) egy nyitott, elsősorban a végeselem-módszeren alapuló numerikus mérnöki laboratórium. Két fő részből áll, a [http://gmsh.info/ Gmsh] a grafikus környezetet, ami az elő- és utófeldolgozó és a hálógeneráló szerepét tölti be. A megoldó pedig a [http://getdp.info/ GetDP], ami alkalmas 1D-s, 2D-s síkbeli és forgásszimmetrikus és 3D-s sztatikus, szinuszos és harmonikus, időfüggő és sajátértékfeladatok megoldására a végeselem-módszer segítségével.  
  
−
A feladat megoldása során azzal nem foglalkozunk, milyen módon lehet a csőtápvonalba jelet juttatni.
+
Érdekességképpen a GetDP mellett még létezik a [http://onelab.info/GetDDM/ GetDDM], ami egy tartomány dekompozíciós módszeren (optimalizált Schwarz-módszer) alapuló megoldó nagyméretű végeselem-módszeren alapuló feladatokhoz. A másik érdekesség a ONELAB mobilapplikáció, ami lehetővé teszi, hogy mobil eszközök (mobiltelefon, tablet) is használjuk a ONELAB-ot.
  
 
=== A feladat megoldásához szükséges ismeretek ===
 
=== A feladat megoldásához szükséges ismeretek ===
−
* A végeselem-módszer lépései;
+
* A végeselem-módszer lépései és annak elméleti háttere;
−
* A Maxwell-egyenletek teljes rendszerének ismerete (hullámegyenlet ismerete);
+
* Elektrosztatikus terek, Laplace-Poisson-egyenlet;
−
* [https://en.wikipedia.org/wiki/Waveguide Csőtápvonal] működésének ismeret.
+
* ONELAB részeinek (Gmsh, GetDP) ismerete.
  
−
=== A vizsgált csőtápvonal ===
+
=== A vizsgált elrendezés ===
−
A feladat geometriai méretei: <math>a = 2\text{cm}</math> (széles oldal); <math>b = 1\text{cm}</math> (keskeny oldal); <math>L = 16\text{cm}; th = 1\text{mm}</math> (csőtápvonal falvastagsága).
 
  
−
A geometria elkészítését és a beállításokat a feladathoz készült YouTube videóban részletezem.
+
A feladat részletes definiálása a videóban is megtalálható. Emellett készítettem egy háromdimenziós ábrát az elrendezés könnyebb elképzeléséhez és annak méretekkel ellátott keresztmetszetét. A feladat az eltolási szimmetria (<math>Z</math>-tengely mentén nem változik a feladat, vagyis <math>\partial/\partial z = 0</math>) miatt kétdimenziós feladatnak tekinthető. Emellett a geometria jelölt középvonalára is szimmetrikus az elrendezés, így elég a felét vizsgálni. Ezen túl pedig a fém részek elhagyhatók, mert ott az elektromos térerősség értéke nulla. Így elegendő a két fémrész közötti teret kitöltő <math>2.4\cdot\varepsilon_0</math> permittivitású anyagot vizsgálni a megfelelő peremfeltételekkel. Dirichlet-típusú peremfeltételként adjuk meg a külső és belső elektróda potenciálját (külső - <math>0~\text{V}</math>; belső - <math>100~\text{V}</math>). A szimmetriasík Neumann-típusú peremfeltétel lesz, viszont ez előírás nélkül, automatikusan is teljesül jelen feladatnál.
  
−
A feladat megoldásához az elektromos térerősségre felírt Helmholtz-egyenletet<ref name="Istvanffy"> Istvánffy E.: ''Tápvonalak, antennák és hullámterjedés'', Műegyetemi Kiadó, 1997. </ref> oldjuk meg
+
A feladat megoldásához a Laplace-egyenletet oldjuk meg
−
::<math> \Delta\vec{E} + k^2\vec{E} = 0 </math>   
+
::<math> -\,\text{div}\,\varepsilon\,\text{grad}\varphi = 0 </math>   
−
ahol <math>k = \omega\sqrt{\mu\varepsilon}</math> a terjedési együttható és <math>\Delta</math> a [https://hu.wikipedia.org/wiki/Laplace-oper%C3%A1tor Laplace-operátor].
+
ahol <math>\varphi</math> az elektromos skalárpotenciál, a következő peremfeltételekkel
 +
::<math>\Gamma_{\text{D}1} = 0~\text{V}</math>,
 +
::<math>\Gamma_{\text{D}2}= 100~\text{V}</math>,
 +
::<math>\Gamma_{\text{N}}= \frac{\partial \varphi}{\partial n} = 0</math> (homogén Neumann-peremfeltétel).
  
−
Azonban egy csőtápvonal szimulációja előtt érdemes meghatározni a vágási frekvenciát (vagy határfrekvenciát, ami alatt nincs hullámterjedés a csőtápvonalban). A vágási frekvencia a következő összefüggéssel határozható meg<ref name="Istvanffy"></ref><ref name="MikroTech1"> Kolos T., Standeisky I.: ''Mikrohullámú technika I.'', Tankönyvkiadó, 1980. </ref>:
+
== A szimulációval kapott eredmények ==
−
::<math> f_{h,mn} = \frac{1}{2\sqrt{\mu\varepsilon}}\sqrt{\left(\frac{m}{a}\right)^2 + \left(\frac{n}{b}\right)^2}</math>,
+
[[File:CapacitorCalculation AdaptiveMeshing.gif|280px|thumb|right|alt=A háló adaptív finomítása a lokális hiba alapján (ANSYS Maxwell). | A háló adaptív finomítása a lokális hiba alapján (ANSYS Maxwell). <span style="font-size:80%; color:blue;">[Kattints a képre az animáció megtekintéséhez.]</span>]]
−
ahol <math>\mu</math> és <math>\varepsilon</math> a csőtápvonalat kitöltő dielektrikum permeabilitása és permittivitása.
+
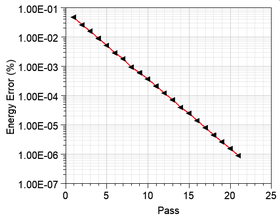
[[File:CapacitorCalculation_EnergyError.png|280px|thumb|right|alt=A globális hiba változása az adaptív lépések függvényében (ANSYS Maxwell). | A globális hiba változása az adaptív lépések függvényében (ANSYS Maxwell).]]
  
−
== A szimulációval kapott eredmények ==
+
Az előbb megadott parciális differenciálegyenlet és peremfeltételekkel előálló feladat megoldásával a következő táblázatban összefoglalt eredmények születtek a kapacitás értékére. A Matlab PDE Toolbox megoldása az előadásból (Gyimóthy Szabolcstól) származik. Gyakorlatilag az összes szoftver azonos megoldásra vezetett. Ilyen szempontból sokkal érdekesebb a végeselemek száma. Az ANSYS Maxwell és 2D Extarctor esetében jelentősen kevesebb a végeselemek száma, mint a többi esetben. Ennek oka az adaptív hálósűrítés<ref name="GyimothyPHD"> Gyimóthy Sz.: ''Adaptív automatikus hálógenerálás a végeselem módszerhez'', PhD disszertáció, 2003.</ref>, amit a két Ansys szoftver alkalmaz az elektrosztatika példák esetében. Ennek köszönhetően ott lesz sűrűbb a felbontás, ahol az szükséges. Az adaptív hálósűrítésre mutat példát a jobb oldali ábra. Alatta pedig a feladat teljes tartományára számított (globális) hiba változása látható.
−
[[File:S11S21 Parameter.png|500px|thumb|right|alt=A bemeneti reflexió (<math>\text{S}_{11}</math> paraméter) és az előre irányú átviteli tényező (<math>\text{S}_{21}</math> paraméter) a frekvencia függvényében. | A bemeneti reflexió (<math>\text{S}_{11}</math> paraméter) és az előre irányú átviteli tényező (<math>\text{S}_{21}</math> paraméter) a frekvencia függvényében.]]
+
{| class="wikitable" align=center style="text-align: center; width: 800px; height: 100px;"
 +
|+ A vizsgált elrendezés kapacitása.
 +
!
 +
! Matlab PDE Toolbox
 +
! ONELAB
 +
! Maxwell 2D
 +
! 2D Extractor
 +
! FEMM
 +
! Agros2D
 +
|-
 +
! Végeselemek száma
 +
| 2944 || 2598 || 740 || 258 || 7885 || 2432
 +
|-
 +
! Kapacitás [<math>\text{pF/m}</math>]
 +
| 173.51 || 173.78 || 173.33 || 173.29 || 173.70 || 173.64
 +
|}
  
−
A levegővel kitöltött csőtápvonalnál <math>\text{TE}_{10}</math> (ejtsd: ''té e egy nulla'') módus esetében a vágási frekvencia
+
Mindegyik esetben lineáris háromszög elemekkel lett felbontva a vizsgált tartomány. A lineáris végeselemekből következik, hogy a végeselemen belül a <math>\varphi</math> potenciál értéke lineárisan változik, vagyis az elektromos térerősség (<math>\vec{E}=\text{grad}\varphi</math>) konstans a végeselemen belül. Ez jól megfigyelhető az alábbi két ábrán. A baloldali ábrán a kapott skalárpotenciálból számított elektromos térerősség [https://en.wikipedia.org/wiki/Norm_(mathematics)#Euclidean_norm euklideszi normája] látható. A jobb oldali ábrán pedig ugyanez az eredmény a simítást (smoothing) követően.
−
::<math> f_{h,10} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}}\sqrt{\left(\frac{1}{0,02}\right)^2 + \left(\frac{0}{0,01}\right)^2} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}\cdot0,02}= 7,4926\text{GHz} \approx 7,5\text{GHz}</math>.
 
  
−
A bemeneti reflexió és az előre irányú átviteli tényező frekvenciafüggvényén (jobb oldali ábra) jól látható, hogy a szimulációval visszakaptuk az előzőleg analitikusan kiszámolt vágási frekvenciát. A vágási frekvenciát követően az átvitel eléri a maximumát.
+
<gallery caption="Az elektromos térerősség a vizsgált elrendezésben." widths="400px" heights="300px" >
 +
File:CapacitorCalculation Efield Linear.png| Lineáris közelítés esetén.
 +
File:CapacitorCalculation Efield Linear Smooth.png|A simítást követően.
 +
</gallery>
  
−
Emellett a lenti ábrákon látható az elektromos (baloldali ábra - E field) és mágneses (jobboldali ábra - H field) térerősség a négyszögletes csőtápvonal keresztmetszetében <math>\text{TE}_{10}</math> módusnál. Ezekhez tartozik a két animáció, amelyből látható, hogy az elektromos térerősségnek csak a terjedési irányra merőleges komponense van (<math> E_z = 0 </math>), vagyis itt tényleg egy transzverzális elektromos (<math>\text{TE}</math>) térről van szó.  
+
Legvégül egy-egy ábra az elektromos skalárpotenciálról és az elektromos térerősség vektorairól. Az elektromos skalárpotenciál ábráján jól láthatóak a vezető körül kialakuló ekvipotenciális vonalak. A vektorok esetében jól látható a homogén Neumann-peremfeltétel teljesülése a szimmetrisík mentén.
  
 
{| width=100%
 
{| width=100%
 
|-
 
|-
 
| align=center |
 
| align=center |
−
[[File:TE10 Efield.png|550px]]
+
[[File:CapacitorCalculation_ElectricScalarPotential.png|550px]]
−
| align=center |
 
−
[[File:TE10 Hfield.png|550px]]
 
−
|-
 
−
|align=center | <span style="font-size:88%;">'''Az elektromos térerősség vektorok a bemeneti portnál <math>\text{TE}_{10}</math> módus esetében.'''</span>
 
−
|align=center | <span style="font-size:88%;">'''A mágneses térerősség vektorok a bemeneti portnál <math>\text{TE}_{10}</math> módus esetében.'''</span>
 
−
|}
 
−
{| width=100%
 
−
|-
 
−
| align=center |
 
−
[[File:TE10 Efield Vec Anim.gif|500px]]
 
 
| align=center |
 
| align=center |
−
[[File:TE10 Hfield Vec Anim.gif|500px]]
+
[[File:CapacitorCalculation_ElectricFieldVectors.png|550px]]
 
|-
 
|-
−
|align=center | <span style="font-size:88%;">'''Az elektromos térerősség vektorok a csőtápvonalban <math>\text{TE}_{10}</math> módus esetében.'''</span><span style="font-size:80%; color:blue;">[Kattints a képre az animáció megtekintéséhez.]</span>
+
|align=center | <span style="font-size:88%;">'''Az elektromos skalárpotenciál értéke az elrendezésben.'''</span>
−
|align=center | <span style="font-size:88%;">'''A mágneses térerősség vektorok a csőtápvonalban <math>\text{TE}_{10}</math> módus esetében.'''</span><span style="font-size:80%; color:blue;">[Kattints a képre az animáció megtekintéséhez.]</span>
+
|align=center | <span style="font-size:88%;">'''Az elektromos térerősség vektorai az elrendezésben.'''</span>
 
|}
 
|}
  
 
== References ==
 
== References ==
 
{{reflist}}
 
{{reflist}}

Latest revision as of 17:52, 5 November 2020

Kételektródás elrendezés kapacitásának számítása

A feladat végeselemhálója és a peremek elnevezése.
A feladat végeselemhálója és a peremek elnevezése.
A feladat megoldása ONELAB (Gmsh + GetDP) segítségével.
A feladat megoldása ONELAB (Gmsh + GetDP) segítségével.

Oktató

  • Marcsa Dániel (óraadó)
  • Előadás: -
  • Fogadóóra: egyeztetés alapján

További oktatók:

  • -
  • Fogadóóra: -.

A feladat célja

A feladat geometriája.
A feladat geometriája.
A feladat keresztmetszete a méretekkel.
A feladat keresztmetszete a méretekkel.

A hallgató megismerje a végeselem-módszerhez kapcsolódó főbb lépéseket, mint a geometria elkészítése vagy importálása, anyagparaméterek, peremfeltételek és gerjesztés megadása, eredmények megjelenítése. Emellett pedig bemutasson a hallgatónak egy szabadon hozzáférhető szoftvert, ami nagyon jól használható disszertációk és kutatások során, köszönhetően felhasználóbarát grafikus felületének és tetszőlegesen konfigurálható megoldójának.

A feladat példája Dr. habil Gyimóthy Szabolcs egyetemi docens Elektromágneses terek előadásából származik. Az előadást ajánlom mindenkinek, aki betekintést szeretne kapni a végeselem-módszer elméleti hátterébe, hogy mi az, amit legtöbbször a szoftverek elrejtenek a felhasználó elől.

A példa az előadásban a Matlab PDE Toolbox segítségével kerül megoldásra. Itt a szabadon hozzáférhető ONELAB (Gmsh + GetDP) és a kereskedelmi ANSYS Maxwell szoftverekkel lesz a megoldás bemutatva. Ezen utóbbi szoftver elsősorban az előadásban elhangzott adaptív hálósűrítés miatt.

A ONELAB a neve alapján (Open Numerical Engineering LABoratory) egy nyitott, elsősorban a végeselem-módszeren alapuló numerikus mérnöki laboratórium. Két fő részből áll, a Gmsh a grafikus környezetet, ami az elő- és utófeldolgozó és a hálógeneráló szerepét tölti be. A megoldó pedig a GetDP, ami alkalmas 1D-s, 2D-s síkbeli és forgásszimmetrikus és 3D-s sztatikus, szinuszos és harmonikus, időfüggő és sajátértékfeladatok megoldására a végeselem-módszer segítségével.

Érdekességképpen a GetDP mellett még létezik a GetDDM, ami egy tartomány dekompozíciós módszeren (optimalizált Schwarz-módszer) alapuló megoldó nagyméretű végeselem-módszeren alapuló feladatokhoz. A másik érdekesség a ONELAB mobilapplikáció, ami lehetővé teszi, hogy mobil eszközök (mobiltelefon, tablet) is használjuk a ONELAB-ot.

A feladat megoldásához szükséges ismeretek

  • A végeselem-módszer lépései és annak elméleti háttere;
  • Elektrosztatikus terek, Laplace-Poisson-egyenlet;
  • ONELAB részeinek (Gmsh, GetDP) ismerete.

A vizsgált elrendezés

A feladat részletes definiálása a videóban is megtalálható. Emellett készítettem egy háromdimenziós ábrát az elrendezés könnyebb elképzeléséhez és annak méretekkel ellátott keresztmetszetét. A feladat az eltolási szimmetria ([math]Z[/math]-tengely mentén nem változik a feladat, vagyis [math]\partial/\partial z = 0[/math]) miatt kétdimenziós feladatnak tekinthető. Emellett a geometria jelölt középvonalára is szimmetrikus az elrendezés, így elég a felét vizsgálni. Ezen túl pedig a fém részek elhagyhatók, mert ott az elektromos térerősség értéke nulla. Így elegendő a két fémrész közötti teret kitöltő [math]2.4\cdot\varepsilon_0[/math] permittivitású anyagot vizsgálni a megfelelő peremfeltételekkel. Dirichlet-típusú peremfeltételként adjuk meg a külső és belső elektróda potenciálját (külső - [math]0~\text{V}[/math]; belső - [math]100~\text{V}[/math]). A szimmetriasík Neumann-típusú peremfeltétel lesz, viszont ez előírás nélkül, automatikusan is teljesül jelen feladatnál.

A feladat megoldásához a Laplace-egyenletet oldjuk meg

[math] -\,\text{div}\,\varepsilon\,\text{grad}\varphi = 0 [/math]

ahol [math]\varphi[/math] az elektromos skalárpotenciál, a következő peremfeltételekkel

[math]\Gamma_{\text{D}1} = 0~\text{V}[/math],
[math]\Gamma_{\text{D}2}= 100~\text{V}[/math],
[math]\Gamma_{\text{N}}= \frac{\partial \varphi}{\partial n} = 0[/math] (homogén Neumann-peremfeltétel).

A szimulációval kapott eredmények

A háló adaptív finomítása a lokális hiba alapján (ANSYS Maxwell).
A háló adaptív finomítása a lokális hiba alapján (ANSYS Maxwell). [Kattints a képre az animáció megtekintéséhez.]
A globális hiba változása az adaptív lépések függvényében (ANSYS Maxwell).
A globális hiba változása az adaptív lépések függvényében (ANSYS Maxwell).

Az előbb megadott parciális differenciálegyenlet és peremfeltételekkel előálló feladat megoldásával a következő táblázatban összefoglalt eredmények születtek a kapacitás értékére. A Matlab PDE Toolbox megoldása az előadásból (Gyimóthy Szabolcstól) származik. Gyakorlatilag az összes szoftver azonos megoldásra vezetett. Ilyen szempontból sokkal érdekesebb a végeselemek száma. Az ANSYS Maxwell és 2D Extarctor esetében jelentősen kevesebb a végeselemek száma, mint a többi esetben. Ennek oka az adaptív hálósűrítés[1], amit a két Ansys szoftver alkalmaz az elektrosztatika példák esetében. Ennek köszönhetően ott lesz sűrűbb a felbontás, ahol az szükséges. Az adaptív hálósűrítésre mutat példát a jobb oldali ábra. Alatta pedig a feladat teljes tartományára számított (globális) hiba változása látható.

A vizsgált elrendezés kapacitása.
Matlab PDE Toolbox ONELAB Maxwell 2D 2D Extractor FEMM Agros2D
Végeselemek száma 2944 2598 740 258 7885 2432
Kapacitás [[math]\text{pF/m}[/math]] 173.51 173.78 173.33 173.29 173.70 173.64

Mindegyik esetben lineáris háromszög elemekkel lett felbontva a vizsgált tartomány. A lineáris végeselemekből következik, hogy a végeselemen belül a [math]\varphi[/math] potenciál értéke lineárisan változik, vagyis az elektromos térerősség ([math]\vec{E}=\text{grad}\varphi[/math]) konstans a végeselemen belül. Ez jól megfigyelhető az alábbi két ábrán. A baloldali ábrán a kapott skalárpotenciálból számított elektromos térerősség euklideszi normája látható. A jobb oldali ábrán pedig ugyanez az eredmény a simítást (smoothing) követően.

  • Az elektromos térerősség a vizsgált elrendezésben.

  • Lineáris közelítés esetén.

  • A simítást követően.

Legvégül egy-egy ábra az elektromos skalárpotenciálról és az elektromos térerősség vektorairól. Az elektromos skalárpotenciál ábráján jól láthatóak a vezető körül kialakuló ekvipotenciális vonalak. A vektorok esetében jól látható a homogén Neumann-peremfeltétel teljesülése a szimmetrisík mentén.

CapacitorCalculation ElectricScalarPotential.png

CapacitorCalculation ElectricFieldVectors.png

Az elektromos skalárpotenciál értéke az elrendezésben. Az elektromos térerősség vektorai az elrendezésben.

References

  1. ↑ Gyimóthy Sz.: Adaptív automatikus hálógenerálás a végeselem módszerhez, PhD disszertáció, 2003.
Retrieved from "http://wiki.maxwell.sze.hu/index.php?title=Kapacitás_számítása&oldid=2544"