Difference between revisions of "Féléves feladat"
(→A mágnesszelep dugattyujára ható erő számítása végeselem-módszerrel) |
(→A mágnesszelep dugattyujára ható erő számítása végeselem-módszerrel) |
||
| Line 60: | Line 60: | ||
== Feladat I. része == | == Feladat I. része == | ||
==== A mágnesszelep dugattyujára ható erő számítása végeselem-módszerrel ==== | ==== A mágnesszelep dugattyujára ható erő számítása végeselem-módszerrel ==== | ||
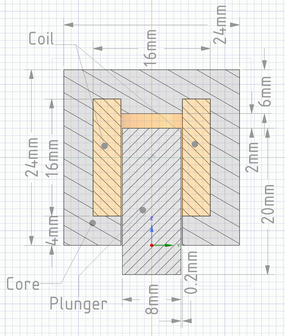
| − | + | [[File:ProblemGeometry.png|285px|thumb|left|alt=A feladat geometriája.|A feladat geometriája.]] | |
| − | A feladat hengerszimmetrikus a | + | A feladat hengerszimmetrikus a függőleges tengelyre, így ennek megfelelően kell elkészíteni a háromdimenziós geometriát a megadott méretek szerint (lásd az ábrán). |
* A megadott paraméterek alapján meghatározni a feladat típusát. | * A megadott paraméterek alapján meghatározni a feladat típusát. | ||
* A feladat elkészítése és futtatása az [https://www.ansys.com/products/3d-design/ansys-aim ANSYS Discovery AIM] programban: | * A feladat elkészítése és futtatása az [https://www.ansys.com/products/3d-design/ansys-aim ANSYS Discovery AIM] programban: | ||
Revision as of 19:21, 5 March 2019
|
Féléves feladat - Mágnesszelep vizsgálata | |
|
Oktató
|
További oktatók:
|
A feladat célja
A hallgatók elsajátítsák az elektromágneses térszámítás alapjait, főbb lépéseit, valamint gyakorlatot szerezzen az eredmények kiértékelésében és a nemzetközi elvárásoknak megfelelő Műszaki Jelentés (Technical Report) írásában.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A sztatikus mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- A geometria elkészítéséhez CAD rendszer ismerete;
- Az ANSYS AIM Student letöltése és telepítése.
A féléves feladat
A feladat két részből áll, egy alapfeladatból, amely hibátlan megoldásával maximum 70%, és egy plusz feladatból, amivel további maximum 30% érető el.
| Leadási határidő: | 2018. november 25., 12:00 |
| Leadás formája: | PDF formátumban. A színes ábrákat úgy kell elkészíteni, hogy fekete-fehérben kinyomtatva is világos legyen a tartalmuk az olvasó számára. |
| Benyújtás nyelve: | Magyar |
| Benyújtás helye: | marcsa@maxwell.sze.hu e-mail címre |
| Késői benyújtás: | Minden megkezdett nap után 5% levonás az elért eredményből (azaz pl. 5 nap késés után 100%-os leadandóra már csak max. 100% - 5x5% = 75%-ot lehet szerezni). |
| Értékelés: | 0 – 50% - Elégtelen (1) |
| 51 – 60% - Elégséges (2) | |
| 61 – 70% - Közepes (3) | |
| 71 – 85% - Jó (4) | |
| 86 – 100% - Jeles (5) | |
| A formai követelmények tekintetében itt is az áramlástan és a mechanika résznél megismert elvárások érvényesek. | |
Feladat I. része
A mágnesszelep dugattyujára ható erő számítása végeselem-módszerrel
A feladat hengerszimmetrikus a függőleges tengelyre, így ennek megfelelően kell elkészíteni a háromdimenziós geometriát a megadott méretek szerint (lásd az ábrán).
- A megadott paraméterek alapján meghatározni a feladat típusát.
- A feladat elkészítése és futtatása az ANSYS Discovery AIM programban:
- a számítási tartomány bemutatása;
- a peremfeltételek (boundary conditions) megállapítása;
- a numerikus módszer idevágó részleteinek leírása (i.e. a FEM (Finite Element Method) program numerikus részletei és a specifikus – azaz ehhez a problémához alkalmazott - beállítási paraméterek felsorolása, megállapítása);
- a FEM szimulációk futtatása;
- az eredmények validálása 2mm-es légrés esetében a dugattyúra ható erő értéke: [math]F(z=2\text{mm}) = XX~\text{N}[/math] (induktivitás [math]L(z=2\text{mm}) = XX~\text{H}[/math]);
- a megoldó beállításainak vizsgálata (Solution performance tuning, Curved surface meshing) az erő függvényében;
- a végeselemek száma (Tetrahedra), az energia (Total Energy), az energiahiba (Energy Error) és az energiahiba megváltozása (Delta Energy) az adaptív lépések függvényében;
- az erő és induktivitás meghatározása;
- az eredmények feldolgozása (post-processing):
- az ekvipotenciális vonalak megjelenítése;
- a mágneses fluxussűrűség mamximumának és minimumának megjelenítése;
- a mágneses térerősség értékének megjelenítése;
- a mágneses fluxussűrűség vektorok megjelenítése;
- Egy Műszaki Jelentés (Technical Report) elkészítése a 3. Szakaszban megadott instrukciók alapján.
Megj.: Az “1. Feladat” elemei a gyakorlat során részletesen áttekintésre kerülnek. Hogyan kell egy elektromágneses feladat szimulációs modelljét elkészíteni és számítógépen lefuttatni. Ez alapján a hallgatók könnyedén tudják az “1. Feladatot” teljesíteni, ha látogatják a gyakorlatokat.
- A feladathoz tartozó paraméterek:
- Levegő és tekercs relatív permeabilitása [math]\mu_r = 1[/math];
- A tekercs áramsűrűsége gerjesztése: [math]I = 0.76~\text{A}[/math], [math]N = 789~\text{menet}[/math];
- A vasmag és a szelep mágnesezési görbéje:
H [A/m] 0 460 640 720 890 1280 1900 3400 6000 10000 20000 B [T] 0 0,8 0,95 1,0 1,1 1,25 1,4 1,55 1,65 1,7 1,72
Feladat II. része
A szelep mozgó részére ható erő és a tekercs induktivitásának meghatározása az elmozdulás függvényében.
Megjegyzés: Ez a feladat a belsőégésű motorokban található mágnesszelepnek felel meg, ami a befecskendezést vezérli.
- Konkrét feladatok
- A dugattyú mozgásának figyelembevétele a kezdeti állapothoz képest [math]-1,8\text{mm-től}\, 10\text{mm-ig}[/math] (legalább 7 pozícióban). Részletes instrukciók a megoldással kapcsolatban nem lesznek.
- Ez a részfeladat azt szándékozik lemérni, hogy mennyire önálló, kezdeményező és szorgalmas a hallgató, azaz:
- képes-e a hallgató önálló munka elvégzésére;
- a szimulációt egyedül megtervezni, összeállítani és lefuttatni.