Difference between revisions of "1. lecke példája"
(→Példa megoldása) |
(→Példa megoldása) |
||
| Line 99: | Line 99: | ||
* '''Tekercs:''' Réz, aminek a relatív premeabilitása jó közelítéssel 1, az áramsűrűséget (''Source Current Density'') pedig a fenti összefügéssel határozzuk meg ['''Mértékegységre figyelj!''']. | * '''Tekercs:''' Réz, aminek a relatív premeabilitása jó közelítéssel 1, az áramsűrűséget (''Source Current Density'') pedig a fenti összefügéssel határozzuk meg ['''Mértékegységre figyelj!''']. | ||
* '''Lezárás:''' Levegő, aminél a relatív permeabilitás szintén 1. | * '''Lezárás:''' Levegő, aminél a relatív permeabilitás szintén 1. | ||
| − | A gerjesztés másik megadási módja a ''Properties/Circuits'' menünél deifinálni a tekercset, majd megadni hozzá a menetszámot. Ebben az esetben a FEMM automatikusan számolja a tekercshez kapcsolódó paramétereket (pl. induktivitás, fluxuskapcsolódás). A peremfeltétel (''Properties/Boundary'') ennél a példánál a feladat megoldásához használt <math>\vec{A}</math> mágneses vektorpotenciál közvetlen előírása (''Prescribed A'') a peremen (Dirichlet vagy elsőfajú). A vektorpotenciál értéke nulla a peremen, ami annyit jelent, hogy a <math>\vec{B}</math> mágneses fluxussűrűségnek csak tangenciális irányú komponense van.<br /> | + | A gerjesztés másik megadási módja a ''Properties/Circuits'' menünél deifinálni a tekercset, majd megadni hozzá a menetszámot. Ebben az esetben a FEMM automatikusan számolja a tekercshez kapcsolódó paramétereket (pl. induktivitás, fluxuskapcsolódás). A peremfeltétel (''Properties/Boundary'') ennél a példánál a feladat megoldásához használt <math>\vec{A}</math> mágneses vektorpotenciál közvetlen előírása (''Prescribed A'') a peremen (Dirichlet vagy elsőfajú). A vektorpotenciál értéke nulla a peremen, ami annyit jelent, hogy a <math>\vec{B}</math> mágneses fluxussűrűségnek csak tangenciális irányú komponense van.<br /> Ha definiáltuk az anyagokat és a peremfeltételt az ''Operation/Block'' menüre váltva megadjuk a feladat tartományait. Majd a tartományok (''Block'') vagy peremek (''Segment'') jobb egérgombbal történő kijelölése utána a Space lenyomásával tudjuk definiálni a tartományhoz / peremhez tartozó anyagot / peremfeltételt. |
| align=center style="width: 4%; | | | align=center style="width: 4%; | | ||
| align=left style="width: 48%; |[[File:Pelda_Geometry_CrossSection.png|285px|thumb|left|alt=Az üzemanyag befecskendező mágnesszelep geometriájának keresztmetszete. |Az üzemanyag befecskendező mágnesszelep geometriájának keresztmetszete.]] A Discovery AIM | | align=left style="width: 48%; |[[File:Pelda_Geometry_CrossSection.png|285px|thumb|left|alt=Az üzemanyag befecskendező mágnesszelep geometriájának keresztmetszete. |Az üzemanyag befecskendező mágnesszelep geometriájának keresztmetszete.]] A Discovery AIM | ||
Revision as of 15:23, 3 July 2019
|
Üzemanyag befecskendező mágnesszelep | |
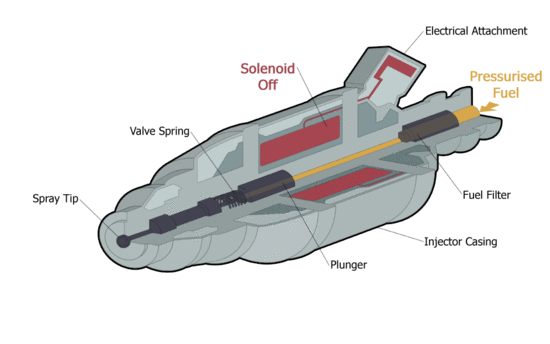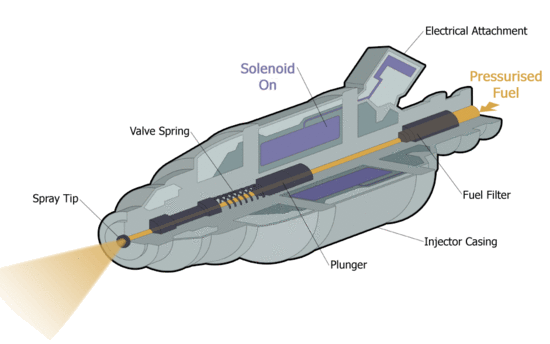
| Az üzemanyag befecskendező működés közben. [1] | Az üzemanyag befecskendezőnél a B vektorok a szolenoid bekapcsolását követően. |
|
| |
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása az üzemanyag befecskendező szolenoidjának szimulációján keresztül.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A sztatikus mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- A geometria elkészítéséhez CAD rendszer ismerete.
A feladat megoldásának lépései
Az ANSYS AIM elindítását követően kiválasztjuk az elektromágneses (Electromagnetics) feladatot a Start gombra kattintva.
A következőkben bemutatott lépésektől eltérően is megvalósítható a feladat. Az AIM használata során a feladat elkészítésében segítséget nyújtanak a különböző lépések során megjelenő üzenetek.
A geometria elkészítése
A feladat geometriáját SpaceClaim-ben, de akár más CAD szoftver segítségével (AutoCAD; SolidWorks; Solid Edge; Catia; Creo; ...) is elkészíthető. A geometria három részből áll, a vasmagból, a tekercsből és a tekercs keresztmetszetéből a gerjesztés megadásához.
A hengeralakú vasmag méretei 14mm magas és 3,6mm a sugara. A tekercs méretei: 20mm magas, 4mm a belső sugár és 10mm a külső sugár.
Geometria elkészítése SpaceClaim-ben
A SpaceClaim megfelelő használatához a Help menüje és a YouTube-on található videók nagy segítséget jelentenek. Itt csak a tekercs keresztmetszetének elkészítését részletezem. Az előadáson és hozzá kapcsolódó gyakorlaton bemutatásra kerül a teljes feladat elkészítése.
Először egy síkor hozunk létre a tekercs-vasmag elrendezés keresztmetszetében a Design - Plane ikon segítségével. Ezt követően a baloldalon található Szerkezet (Structure) ablakban a Tervkomponensre (struktúra fa gyökérébe) kattintva hozzáadunk egy új komponenst (New Component). Az új komponens tulajdonságai között (új komponensre kattintva Tulajdonságok (Properties)) a Topológia megosztása (Shared Topology) legyen Megosztásra (Shared) állítva. Ha ezt megtettük, a tekercset húzzuk bele az új komponensbe. Majd a következő lépésként rajzoljuk meg a tekercs keresztmetszetét felhasználva az elrendezés metszeti nézetét. Ha megrajzoltuk a tekercs keresztmetszetét, annak is az új komponens fájában kell lennie. Ennek köszönhetően az ANSYS Discovery AIM a megrajzolt felületet a tekercs keresztmetszeteként fogja kezelni, így erre a felületre előírható a gerjesztés. Végül a Tervkomponensre kattintva jobbegérgombbal válasszuk ki az Aktív komponens (Active Component) lehetőséget, hogy a teljes geometria aktív legyen, ne csak az újonnan létrehozott komponens. Valamint itt lehet paraméterezni a geometria méreteit és egymáshoz képesti helyzetét, tehát például a vasmag mozgásának figyelembevételét.
Ha ezzel végeztünk mentsük el a geometriát, majd zárjuk be a SpaceClaim-et és indítsuk el az ANSYS Discovery AIM-et, azon belül pedig válasszuk az Electromagnetics lehetőséget. Ezt követően végigvezet minket a teljes szimuláción, így a szimuláció minden lépése szintén nem kerül részletezésre.
A geometria importálását követően a feladat típusa Electromagnetic, a forrás Applied current és DC. A feladat termikus viselkedése Constant temperature és opcióként válasszuk ki az erő (Compute force) és induktivitás (Compute inductance) számítást. Majd legvégül válasszuk a Create surround automatically opciót. Ez a lehetőség akkor fontos, ha a méretek vagy pozíció változni fog a szimuláció során.
A feladat definiálása
Az anyagokat az egyes térfogatok kiválasztásával tudjuk definiálni.
A tekercs anyaga réz (Copper), a vasmagé 1008-as acél (Steel 1008). Amennyiben ezeknek valamilyen tulajdonságát (vezetőképesség, B-H görbe) módosítani szeretnénk, azt később megtehetjük az anyagok tulajdonságainál.
Ezt követően a gerjesztést kell definiálni. Ehhez a tekercs keresztmetszetének rajzolt felületet kell kiválasztani, majd az áram erősségét (0,2A) és a menetszámot (2000) kell megadni. Itt definálható a tekercs kitöltési tényezője is.
Ha ezzel is megvagyunk, a diszkretizálással és a megoldó beállításaival nincs teendő, az alapbeállítások megfelelőek lesznek, futtatható a feladat. Adaptív hálózás történik a megoldás során, ezért nem foglalkozunk ennél a feladatnál a végeselemháló beállításával.
Az eredmények kiértékelése
A különböző térváltozók felületre / térfogatba való kirajzoltatásán túl itt tudjuk megnézni a vasmagra ható erő értékét és a tekercs induktivitását. Erre a két mennyiségre a következő értékek jöttek ki, a keresztmetszeti ábrának megfelelő elrendezést tekintjük 15mm-nek, valamint ahhoz képest -15mm-rel (0 mm pozíció) a [math]z[/math]-tengely irányában kimozdítva a vasmagot.
| Pozíció | 0 mm | 15 mm |
|---|---|---|
| Induktivitás [mH] | 23,97 | 52,07 |
| Erő [mN] | 22,132 | 9,7617 |
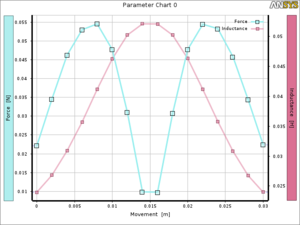
Emellett lehetséges a különböző változókat (pozíció, méret, áram, menetszám, ...) paraméterezni. Egy ilyen szimulációnak az eredménye látható az ábrán, ahol a vasmag tekercshez képesti pozíciója lett paraméterezve. Ennek köszönhetően automatikusan történik a paraméter megváltoztatása és a szimuláció futtatása.
Példa megoldása
A következőkben a mágnesszelep megoldása és az eredmények kiértékelése kerül bemutatásra.
| Finite Elemenet Method Magnetics | ANSYS Discovery AIM | ||
| A FEMM szoftver használatához segítséget nyújt a következő két videó: | A Discovery AIM szoftver használatához segítséget nyújt a következő három videó: | ||
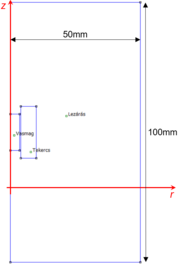
| A FEMM kétdimenziós feladatok (síkbeli vagy hengerszimmetrikus) megoldására alkalmas. A vizsgált példa hengerszimmetrikus mágneses feladat. Ezért a Create a new problem ablakban a Magnetics Problem feladattípust kell választani. Ezt követően érdemes elsőnek a Problem menüre kattintva megadni a feladat típusát (Problem Type - Axisymmetric), a hossz mértékegységét (Length Units - Milimeters). A többi paraméter maradhat az alapbeállítás, de például frekvenciatartománybeli (harmonikus) feladat esetében itt lehet specifikálni a gerjesztés frekvenciáját. A geometria elkészítésénél először a pontokat, majd a különböző tartományokat határoló vonalakat kell definiálni. A pontok a kurzor segítségével is elhelyezhetők, azonban ennek pontossága függ a rácspont sűrűségétől. Ezért célszerűbb a tabulátort (Tab) használni, ahol pontosan megadható a pont két koordinátája. Jelen (hengerszimmetrikus) esetben az a két koordináta az r (vízszintes) és a z (függőleges) koordináta. Majd a pontok a kurzor segítségével összeköthetőek, miután az Operation/Node menüről átváltunk az Operation/Segment műveletre. Az ábrán látható elrendezést kell kapnunk, ami már tartalmazza a lezárást is (100mm x 50mm). A következő lépés az anyagok (Properties/Materials) és a feladatnál használt peremfeltétel (Properties/Boundary) definiálása. Ennél a példánál az anyagparaméternél adjuk meg a gerjesztést is mint áramsűrűség. A [math]J[/math] áramsűrűséget a következő összefüggésel tudjuk meghatározni:
ahol [math]N[/math] a menetszám, [math]I[/math] az egy menetre jutó áramerősség és [math]A[/math] a tekercs keresztmetszete.
A gerjesztés másik megadási módja a Properties/Circuits menünél deifinálni a tekercset, majd megadni hozzá a menetszámot. Ebben az esetben a FEMM automatikusan számolja a tekercshez kapcsolódó paramétereket (pl. induktivitás, fluxuskapcsolódás). A peremfeltétel (Properties/Boundary) ennél a példánál a feladat megoldásához használt [math]\vec{A}[/math] mágneses vektorpotenciál közvetlen előírása (Prescribed A) a peremen (Dirichlet vagy elsőfajú). A vektorpotenciál értéke nulla a peremen, ami annyit jelent, hogy a [math]\vec{B}[/math] mágneses fluxussűrűségnek csak tangenciális irányú komponense van. |
A Discovery AIM | ||
| A FEMM | A Discovery AIM | ||
| A FEMM | A Discovery AIM | ||
| A FEMM | A Discovery AIM | ||
|
jdjdjdjd djdjdjdjd dddjdjjdd dkdkdkdkdk |
|||
| A tekercs körül kialakuló mágneses térerősség (ANSYS Discovery AIM). | Az örvényáram veszteség az öntöttvas rúd felületén (ANSYS Discovery AIM). |