Difference between revisions of "Feladat 5"
(→Induktivitás meghatározása) |
(→A hővezetés differenciálegyenlete) |
||
| Line 163: | Line 163: | ||
==== A hővezetés differenciálegyenlete ==== | ==== A hővezetés differenciálegyenlete ==== | ||
| − | + | A hővezetés általános differenciálegyenletéhez az energimegmaradás tételét a hővezetés jelenségére alkalmazva jutunk.</ br> | |
| + | Vizsgáljuk egy <math>V</math> térfogatú hővezető közeg energiaegyensúlyát. A térfogatba foglalt közeg: | ||
| + | |||
| + | <math>m = \int_{V}\rho~\text{d}V</math>, | ||
| + | |||
| + | ahol <math>\rho</math> a sűrűség [kg/m3]. | ||
<math>L = \frac{2\cdot W_{\text{m}}}{I^{2}}</math>, | <math>L = \frac{2\cdot W_{\text{m}}}{I^{2}}</math>, | ||
Revision as of 13:50, 13 October 2020
|
Feladat #5 - Stacionárius hőáramlás | ||
|
Oktató
|
További oktatók:
| |
A feladat célja
A hallgatók elsajátítsák az elektromágneses térszámítás alapjait, főbb lépéseit, valamint gyakorlatot szerezzen az eredmények kiértékelésében a FEMM vagy az Agros2D szoftver segítségével. Ezen túl a nemzetközi elvárásoknak megfelelő Műszaki Jelentés (Technical Report) írásában is gyakorlatot szerezzen.
A feladat egy söntellenállásnál meghatározni a feszültségesést, az ellenállást és a keletkező veszteségeket adott áramerősség mellett.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A stacionárius áramlási térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés és peremfeltétel megadásához);
- A FEMM vagy Agros2D szoftver alapszintű kezelése.
A feladat
A feladat két részből áll, a szimulációból és az összefoglaló elkészítéséből.
| Leadási határidő: | nappali - 2020. december 5. 23:59 / távoktatás - 2020. december 5. 23:59 |
| Leadás formája: | A szimulációs fájlt (FEMM - *.feh; Agros2D - *.a2d) tömörítve (.zip formátumban). Az összefoglalót PDF formátumban. A színes ábrákat úgy kell elkészíteni, hogy fekete-fehérben kinyomtatva is világos legyen a tartalmuk az olvasó számára. |
| Benyújtás nyelve: | Magyar |
| Benyújtás helye: | A Moodle rendszerben kiírt feladatnál. |
| Késői benyújtás: | Minden megkezdett nap után 5% levonás az elért eredményből (azaz pl. 5 nap késés után 100%-os leadandóra már csak max. 100% - 5x5% = 75%-ot lehet szerezni). |
| Értékelés: | 0 – 50% - Elégtelen (1) |
| 51 – 60% - Elégséges (2) | |
| 61 – 70% - Közepes (3) | |
| 71 – 85% - Jó (4) | |
| 86 – 100% - Jeles (5) | |
| A formai követelmények tekintetében az alábbi linken elérhető útmutatót/sablont kell használni. | |
Feladat I. része
Rezisztencia és veszteség számítása végeselem-módszerrel
A kapott sorszám alapján a feladat geometriájának méreteit a következő táblázatban találja: Feladat #3 méretei.
A feladat: meghatározni az elrendezés esetében a feszültségesést, a rezisztenciát és az ohmos veszteséget.
A feszültségesés az elrendezés két kapcsa között lévő potenciálkülönbség. A rezisztenciát az Ohm-törvény segítségével tudja meghatározni:
[math]R = \frac{U}{I}[/math],
majd a veszteség
[math]P = I^2\cdot R[/math]
képlettel, ahol [math]U[/math] a feszültségesés, [math]I[/math] az áramerősség, [math]R[/math] a rezisztencia.
A [math]z-[/math]irányú hossza (vastagsága) a feladatnak minden esetben [math]5\,\text{mm}[/math] legyen.
| Anyag | Titánium | Réz | Aluminium | Réz mangán |
|---|---|---|---|---|
| [math]\sigma~[\text{MS/m}][/math] | 1,789 | 58 | 36,9 | 20,833 |
Elvégzendő feladatok
- A megadott paraméterek alapján elkészíteni a síkbeli (planar) feladat geometriáját a FEMM vagy Agros2D szoftverek valamelyikében;
- Az anyagtulajdonságok, a gerjesztés és a peremfeltételek megadása;
- A FEM szimuláció futtatása;
- Az eredmények kiértékelése, ha a [math]z-[/math]irányú hossza a feladatnak minden esetben [math]5\,\text{mm}[/math].
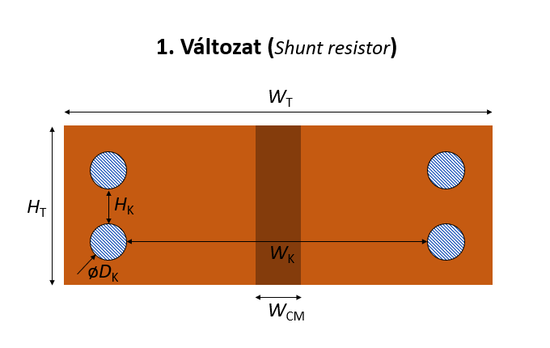
A táblázatban található méretek jelentését az alábbi ábrák mutatják. A táblázatban a 2. oszlop jelöli a változat számát.
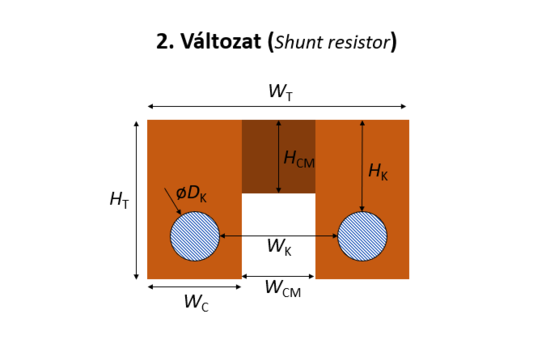
| Feladat #3 - 1. változat. | Feladat #3 - 2. változat. |
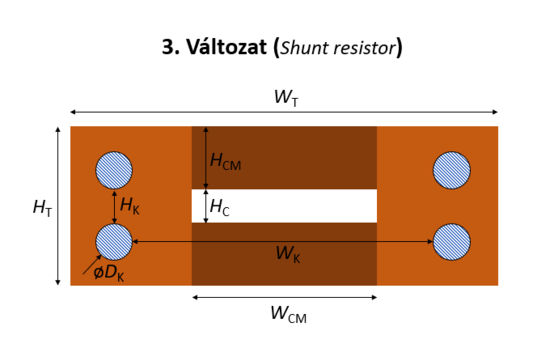
| Feladat #3 - 3. változat. | Feladat #3 - anyagok. |
Szoftverek használatának bemutatása
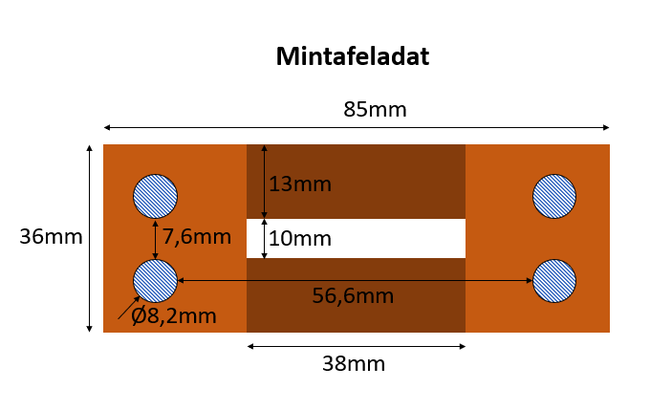
Az 1. ábrán látható feladat megoldásán keresztül röviden bemutatom az előadáson és az önálló feladat során használandó szoftvereket. A feladathoz készült videók segítségével elsajátítható a feladat beállítása, a geometria rajzolása, az anyagtulajdonságok, a peremfeltételek és a gerjesztés megadása. Majd a megoldást követően a térváltozók megjelenítése és a feladathoz kapcsolódó számítandó mennyiségek meghatározása. A feladatban az áramerősség [math]400~\text{A}[/math].
A mintdapéldához nincs a levegő berajzolva. Ennek méretei a videókban megtalálhatóak, de akár gyakorlásképpen ellenőrizhető, hogyan befolyásolja a kapacitás értékét (az eredményt) a lezárás mérete.
| Ábra 1. - A mintapélda és geometriai méretei. |
| Szoftver | FEMM | Agros2D | Maxwell 2D | Maxwell 3D | Q3D Extractor | Discovery AIM | Discovery Live |
|---|---|---|---|---|---|---|---|
| Potenciálkülönbség [mV] | 8,025 | 8,049 | - | 8,028 | 8,022 | - | - |
| Rezisztencia [[math]\mu\Omega[/math]] | 20,064 | 20,125 | 20,071 | 20,056 | 20,054 | - | - |
| Veszteség [W] | 3,21 | 3,22 | 3,21 | 3,21 | 3,21 | - | - |
Videók a szoftverek használatához
- [ FEMM]
- [ Agros2D]
- [ Ansys Maxwell 2D]
- [ Ansys Maxwell 3D]
- [ Ansys Q3D Extractor]
A hővezetés differenciálegyenlete
A hővezetés általános differenciálegyenletéhez az energimegmaradás tételét a hővezetés jelenségére alkalmazva jutunk.</ br> Vizsgáljuk egy [math]V[/math] térfogatú hővezető közeg energiaegyensúlyát. A térfogatba foglalt közeg:
[math]m = \int_{V}\rho~\text{d}V[/math],
ahol [math]\rho[/math] a sűrűség [kg/m3].
[math]L = \frac{2\cdot W_{\text{m}}}{I^{2}}[/math],
ahol [math]W_{\text{m}}[/math] a mágneses energia és [math]I[/math] a tekercs árama (a fenti feladatoknál [math]2~\text{A}[/math]).
Az induktivitás meghatározása során a mágnes ne szerepeljen ([math]B_{\text{r}}=0~\text{T}[/math] és [math]H_{\text{c}}=0~\text{A/m}[/math]) a feladatban!
A fenti példáknál van olyan eset, ahol több tekercs van a feladatban. Ebben az esetben először a következő induktivitás mártix elemeit kell meghatározni
[math]\begin{bmatrix} U_{1} \\ U_{2} \end{bmatrix} = \begin{bmatrix} L_{11} & M_{12}\\ M_{21} & L_{22} \end{bmatrix}\begin{bmatrix} I_{1} \\ I_{2} \end{bmatrix}[/math].
A tekercsek öninduktivitásának ([math]L_{11}[/math] és [math]L_{22}[/math]) meghatározásához, mindig csak egy tekercset kell gerjeszteni, majd a fenti képlettel meghatározni az induktivitást.
A kölcsönös induktivitás ([math]M_{12} = M_{21} = M[/math]) meghatározásához a csatolt áramkörben tárolt energia képletét kell használni:
[math] W_{\text{m}} = \frac{1}{2}\cdot L_{11}\cdot I_1 + \frac{1}{2}\cdot L_{22}\cdot I_2 \pm M\cdot I_1\cdot I_2[/math].
Ebben az esetben mindkettő tekercs gerjesztve van, máskülönben (ha [math]I_1 = 0[/math] vagy [math]I_2 = 0[/math]) visszakapjuk a fenti képletet.
Kölcsönös induktivitás előjele:
Pozitív (+): Mindkettő áram iránya azonos;
Negatív (-): A két áram iránya ellentétes.
A megadott feladatok esetében a két tekercs sorba van kötve. A fenti mátrix redukálásához és a tényleges induktivitáshoz a következő összefüggést kell alkalmazni:
[math] L_{\text{soros}} = (L_{11} + M_{12}) + (M_{21} + L_{22})[/math]
Megjegyzés: Nagyon fontos ismerni a használt képletek, módszerek korlátait. A fenti módszer csak lineáris rendszerek esetében ad helyes eredményt. Mindegyik feladatban található vasmag, amelynek nemlineáris a mágnesezési karakterisztikája. Azonban a feladatok esetében a mágneses fluxussűrűség a nemlineáris vasban nem haladja meg az [math]1~T[/math] értéket, tehát a feladat még jó közelítéssel lineárisnak tekinthető.
Feladat II. része
A műszaki jelentés elkészítése és leadása a Moodle rendszerben PDF formátumban.
A műszaki jelentés a következő linken elérhető: Word; PDF.