Difference between revisions of "Féléves feladat"
(→Feladat II. része) |
(→Feladat I. része) |
||
| Line 121: | Line 121: | ||
[[Image: CAE SA EMSolutions 2022Spring.png | 650px]] | [[Image: CAE SA EMSolutions 2022Spring.png | 650px]] | ||
|- | |- | ||
| − | | align = center | <span style="font-size:88%;>''' '' | + | | align = center | <span style="font-size:88%;>''' ''Ábra 2.'' - Lehetséges megoldások (''Bal - Maxwell 3D, Jobb - Q3D Extractor).'''</span> |
|} | |} | ||
Revision as of 14:17, 17 February 2022
|
Söntellenállás vizsgálata | ||
|
Oktató
|
További oktatók:
| |
A feladat célja
A hallgatók elsajátítsák az elektromágneses térszámítás alapjait, főbb lépéseit, valamint gyakorlatot szerezzen az eredmények kiértékelésében és a nemzetközi elvárásoknak megfelelő Műszaki Jelentés (Technical Report) írásában.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- Az áramvezetési feladatra vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- A geometria elkészítéséhez CAD rendszer ismerete;
- Az Ansys Electronics Desktop Student letöltése és telepítése.
A féléves feladat
A feladat két részből áll, egy alapfeladatból, amely hibátlan megoldásával maximum 80%, és egy plusz feladatból, amivel további maximum 20% érhető el.
Leadási határidő: Lásd a feladatkiírásnál! Leadás formája: PDF formátumban. A színes ábrákat úgy kell elkészíteni, hogy fekete-fehérben kinyomtatva is világos legyen a tartalmuk az olvasó számára. Benyújtás nyelve: Magyar Benyújtás helye: A Moodle rendszerben kiírt feladatnál. Késői benyújtás: Minden megkezdett nap után 5% levonás az elért eredményből (azaz pl. 5 nap késés után 100%-os leadandóra már csak max. 100% - 5x5% = 75%-ot lehet szerezni). Értékelés: 0 – 50% - Elégtelen (1) 51 – 60% - Elégséges (2) 61 – 70% - Közepes (3) 71 – 85% - Jó (4) 86 – 100% - Jeles (5) A formai követelmények tekintetében itt is az áramlástan és a mechanika résznél megismert elvárások érvényesek.
Feladat I. része
Calculating the resistance and the total loss of the shunt resistor by finite element method
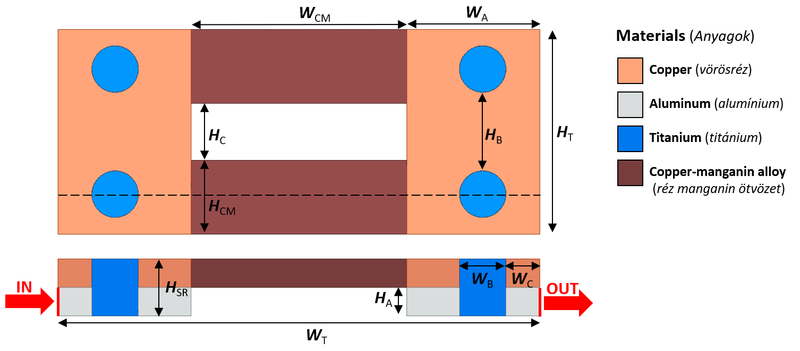
The geometry dimensions for your task you can find in the following table: Semester Assigment.
This task is a DC current conduction problem. The solved equation is
[math]\nabla\cdot\sigma\nabla \varphi=0[/math]
with following boundary conditions
[math]\vec{J}\cdot\vec{n}=-J_{\text{n}}[/math] on [math]\Gamma_{\text{J}}[/math] (This is the input)
and
[math]\varphi=U_0 = \text{0 V}[/math] on [math]\Gamma_{\text{E}}[/math] (This is the output),
where [math]J_{\text{n}}[/math] is the current density calculated from the specified current excitation.
The task: determine the voltage drop, the resistance and the ohmic loss of the problem.
The voltage drop is the potential difference between the two terminals of the arrangement. You can determine resistance using Ohm's law:[math]R = \frac{U}{I}[/math],
then the ohmic loss
[math]P = I^2\cdot R[/math]
where [math]U[/math] is the voltage drop, [math]I[/math] is the current and [math]R[/math] is the resistance.
Bulk conductivity of materials. Material Titanium Copper Aluminum Copper-manganin alloy [math]\sigma~[\text{MS/m}][/math] 1.82 58 38 20.833 Tasks
- Draw the geometry based on the specified dimensions.
- Define the problem based on the given material parameters and boundary conditions;
- Creating and specifying the task geometry in Ansys Electronics Desktop Student;
- Run the FEM simulation;
The parameters listed in the task can be calculated with the Maxwell 3D - DC Conduction solver and the Q3D Extractor - DC solver.
Ábra 2. - Lehetséges megoldások (Bal - Maxwell 3D, Jobb - Q3D Extractor).
A tesztfeladat eredményei. Mennyiségek Feszültségesés [mV] Rezisztencia [[math]\text{n}\Omega[/math]] Veszteség [W] Maxwell 3D 10.9927 18.3211 6.5956 Q3D Extractor 10.9759 18.2931 6.5855
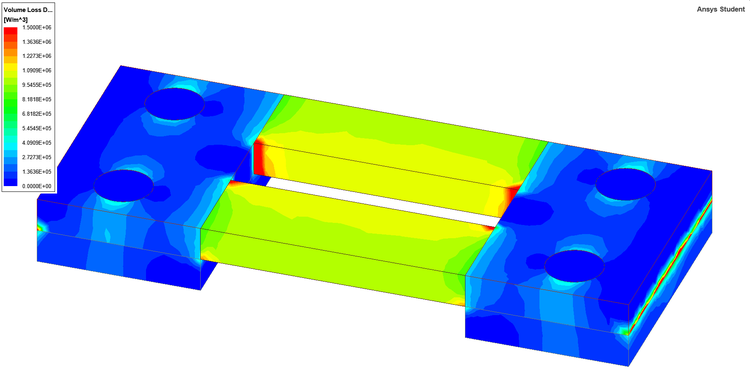
Ansys Maxwell 3D - Az áram okozta veszteség a söntellenállás felületén. Ansys Q3D Extractor - Az áram okozta veszteség a söntellenállás felületén.
Feladat II. része
Az Ansys EM diákverziójában az Icepak ad lehetőséget a termikus jelenségek vizsgálatára. Ansys Icepak egy általános áramlástani megoldó elektronikák (PCB / teljesítménymodul) melegedésének és hűtésének vizsgálatához fejlesztett specifikus képességekkel.
A feladatnál a hűtés természetes konvekció. A gerjesztés az elektromágneses szimulációból származó veszteség.
Anyagok termikus tulajdonságai. Anyag Titánium Réz Alumínium Réz mangán ötvözet [math]\rho~[\text{kg}/\text{m}^3][/math] 4500 8933 2689 8400 [math]c_{\text{P}}~[\text{J}/(\text{kg}\cdot\text{°C})][/math] 522 385 951 410 [math]\lambda~[\text{W}/(\text{m}\cdot\text{°C})][/math] 21 400 237.5 22 A termikus szimulációval kapott eredményeket mutatja a következő táblázat.
A tesztfeladat eredményei. Mennyiségek Max. hőmérséklet [°C] Min. hőmérséklet [°C] Max. sebesség [m/s] Maxwell 3D + Icepak 75.9284 71.3658 0.2881 Q3D Extractor + Icepak 75.8669 71.3002 0.2880
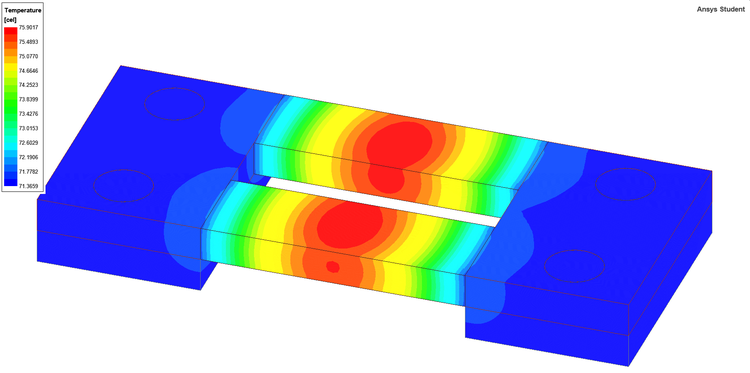
Ansys Maxwell 3D + Ansys Icepak - Hőmérsékleteloszlás a söntellenállás felületén. Ansys Q3D Extractor + Ansys Icepak - Hőmérsékleteloszlás a söntellenállás felületén. A mintafeladat archivált változatát a következő linken találja: Shunt Resistor (Ansys EM Student 2021 R2).