Feladat
|
Feladat #1 - Elektrosztatika | ||
|
Oktató
|
További oktatók:
| |
A feladat célja
A hallgatók elsajátítsák az elektromágneses térszámítás alapjait, főbb lépéseit, valamint gyakorlatot szerezzen az eredmények kiértékelésében a FEMM vagy Agros2D szoftver segítségével. Ezen túl a nemzetközi elvárásoknak megfelelő Műszaki Jelentés (Technical Report) írásában is gyakorlatot szerezzen.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- Az elektrosztatikus térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés és peremfeltétel megadásához);
- A FEMM vagy Agros2D szoftver alapszintű kezelése.
A feladat
A feladat két részből áll, a szimulációból és az összefoglaló elkészítéséből.
| Leadási határidő: | 2020. október 02., 23:59 |
| Leadás formája: | A szimulációs fájlt (FEMM - *.fee; Agros2D - *.a2d) tömörítve (.zip formátumban). Az összefoglalót PDF formátumban. A színes ábrákat úgy kell elkészíteni, hogy fekete-fehérben kinyomtatva is világos legyen a tartalmuk az olvasó számára. |
| Benyújtás nyelve: | Magyar |
| Benyújtás helye: | A Moodle rendszerben kiírt feladatnál. |
| Késői benyújtás: | Minden megkezdett nap után 5% levonás az elért eredményből (azaz pl. 5 nap késés után 100%-os leadandóra már csak max. 100% - 5x5% = 75%-ot lehet szerezni). |
| Értékelés: | 0 – 50% - Elégtelen (1) |
| 51 – 60% - Elégséges (2) | |
| 61 – 70% - Közepes (3) | |
| 71 – 85% - Jó (4) | |
| 86 – 100% - Jeles (5) | |
| A formai követelmények tekintetében az alábbi linken elérhető útmutatót/sablont kell használni. | |
Feladat I. része
Kapacitás számítása végeselem-módszerrel
A kapott sorszám alapján a feladat geometriájának méreteit a következő táblázatban találja: Feladat #1 méretei.
A feladat: meghatározni a vezető (ha több van tetszőlegesen választott vezetőre) esetében a kapacitást és a töltést.
A kapacitást az elektromos energia segítségével tudja meghatározni:
[math]C = \frac{2\cdot W_{\text{e}}}{U^{2}}[/math],
majd a töltést
[math]\rho = C\cdot U[/math]
képlettel, ahol [math]U[/math] a vezetők közötti potenciálkülönbség, [math]\rho[/math] a töltés, [math]W_{\text{e}}[/math] az elektromos energia.
A töltést mindig [math]1\,\text{V}[/math] gerjesztésre határozza meg!
Elvégzendő feladatok
- A megadott paraméterek alapján elkészíteni a síkbeli (planar) feladat geometriáját a FEMM vagy Agros2D szoftverek valamelyikében;
- Az anyagtulajdonságok, a gerjesztés és a peremfeltételek megadása;
- A FEM szimuláció futtatása;
- Az eredmények kiértékelése, ha a [math]z-[/math]irányú hossza a feladatnak minden esetben [math]1\,\text{m}[/math].
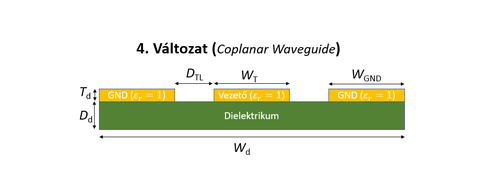
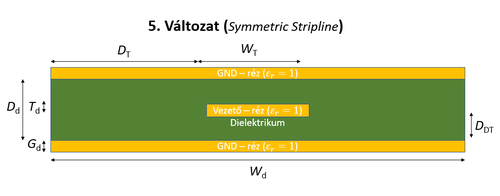
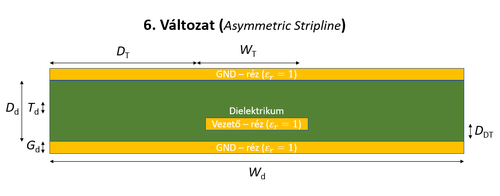
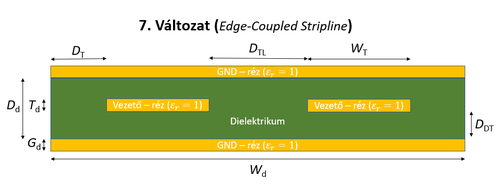
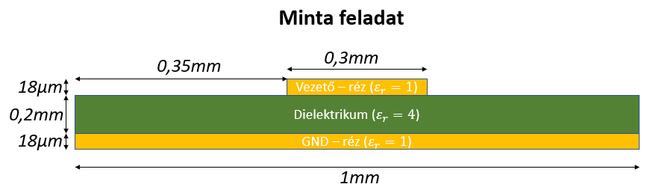
A táblázatban található méretek jelentését az alábbi ábrák mutatják. A táblázatban a 2. oszlop jelöli a változat számát.
| Feladat #1 - 1. változat. | Feladat #1 - 2. változat. |
| Feladat #1 - 3. változat. | Feladat #1 - 4. változat. |
| Feladat #1 - 5. változat. | Feladat #1 - 6. változat. |
| Feladat #1 - 7. változat. | Feladat #1 - 8. változat. |
Szoftverek használatának bemutatása
Az 1. ábrán látható feladat megoldásán keresztül röviden bemutatom az előadáson és a önálló feladat során használandó szoftvereket. A feladathoz készült videók segítségével elsajátítható a feladat beállítása, a geometria rajzolása, az anyagtulajdonságok, a peremfeltételek és a gerjesztés megadása. Majd a megoldást követően a térváltozók megjelenítése és kapacitás valamint töltés meghatározása.
| Ábra 1. - A mintapélda és geometriai méretei. |
| Szoftver | Maxwell 2D | 2D Extractor | FEMM | Agros2D | Analitikus - 1 | Analitikus - 2 |
|---|---|---|---|---|---|---|
| Kapacitás [pF] | 96,162 | 96,918 | 96,399 | 96,020 | 127,9 | 93,040 |
- A megoldó beállításainak vizsgálata (Solution performance tuning, Curved surface meshing) az erő függvényében (AIM); A lezárás méretének és a háló sűrűségének (csomópontok [Nodes] vagy háromszögek [Elements] száma) vizsgálata az erő függvényében (FEMM);
- A végeselemek száma (Tetrahedra; Elements), az energia (Total Energy), az energiahiba (Energy Error - AIM) és az energiahiba megváltozása (Delta Energy - AIM) az adaptív lépések függvényében a két szélső esetben;
- az eredmények feldolgozása (post-processing) [lentiek közül legalább kettő legyen a jelentésben]:
- 1) az erő és induktivitás meghatározása;
- 2) az ekvipotenciális vonalak megjelenítése;
- 3) a mágneses fluxussűrűség maximumának és minimumának megjelenítése;
- 4) a mágneses térerősség értékének megjelenítése;
- 5) a mágneses fluxussűrűség vektorok megjelenítése.
- Egy Műszaki Jelentés (Technical Report) elkészítése a megadott instrukciók alapján, a fenti eredmények felhasználásával.
Megj.: A “Feladat I. részének” elemei a gyakorlat során részletesen áttekintésre kerülnek, hogyan kell egy elektromágneses feladat szimulációs modelljét elkészíteni és lefuttatni. Ez alapján a hallgatók könnyedén tudják a “Feladat I. részét” teljesíteni, ha látogatják a gyakorlatokat.
Megj.: A feladatban a vasmag (Core) és a tekercs (Coil) érintkezik. Ez kétdimenziós (hengerszimmetrikus) feladatnál nem okoz problémát, de a háromdimenziós példánál emiatt az áram nem csak a tekercsben hanem a vasmagban is folyik. Ennek kiküszöbölésére az ANSYS Discovery AIM szoftverben a Physics Definition - Electromagnetic Conditions - Insulating peremfeltételt kell alkalmazni a tekercsre (célszerű a tekercs térfogatára alkalmazni).
A valóságban is szigetelő veszi körül a tekercset, amit jellemzően nem modellezünk a feladatban, helyette peremfeltételt alkalmazunk.
- A feladathoz tartozó paraméterek:
- Levegő és tekercs relatív permeabilitása [math]\mu_r = 1[/math];
- A tekercs gerjesztése (Az eredmények validálásához)): [math]I = 0.76~\text{A}[/math], [math]N = 789~\text{menet}[/math] (egyenfeszültség);
- A vasmag és a szelep mágnesezési görbéje:
Feladat II. része
A műszaki jelentés elkészítése és leadása a Moodle rendszerben PDF formátumban.
A műszaki jelentés a következő linken elérhető: Műszaki jelentés.