Lecture 4.
|
Lecture 4. | |
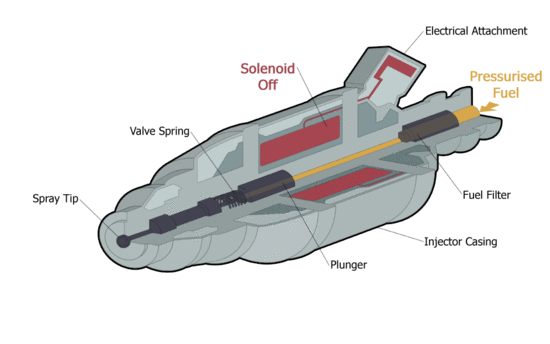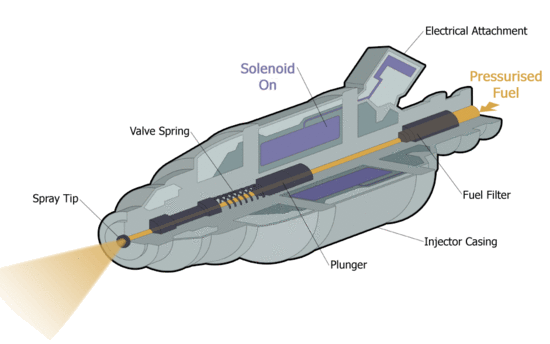
| Animated cut through diagram of a typical fuel injector [1] | Animated cut through diagram of a typical fuel injector [Click to see animation]. |
|
Oktató
|
További oktatók:
|
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása az üzemanyag befecskendező szolenoidjának szimulációján keresztül.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A sztatikus mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- A geometria elkészítéséhez CAD rendszer ismerete.
Boundary Element Method (BEM)[2]
Method of Moments (MoM)[3]
In the 1960s, R.F. Harrington and others applied a technique called the Method of Moments to the solution of electromagnetic field problems. The Method of Moments (also called the Method of Weighted Residuals) is a technique for solving linear equations of the form,
where the functional [math]\mathcal{L}(\bullet)[/math] is a linear operator, [math]f[/math] is a known excitation or forcing function, and [math]\phi[/math] is an unknown quantity. To solve this problem on a digital computer, we start by expressing the unknown solution as a series of basis or expansion functions, [math]v_n[/math],
where [math]a_n[/math] are unknown coefficients describing the amplitude of each term in the series.
Now instead of one equation with a continuous unknown quantity, [math]f[/math], we have an equation with [math]N[/math] scalar unknowns,
[math]\mathcal{a_1v_1+a_2v_2+\dots+a_Nv_N}=f[/math].
To solve for the values of [math]a_n[/math], we need [math]N[/math] linearly independent equations; so [math]a_n[/math] different weighting or testing functions, [math]w_n[/math], are applied. This yields the following system of [math]N[/math] equations in [math]N[/math] unknowns:
This linear system of equations has the form,
[math]\textbf{A}\textbf{x}=\textbf{b} where the elements of \textbf{A} are known quantities that can be calculated from the linear operator, the functional \ltmath\gt\mathcal{L}(\bullet)[/math], and the chosen basis and weighting functions. The elements of \textbf{b} are determined by applying the weighting functions to the known forcing function. The unknown elements of \textbf{x} can be found by solving the matrix equation. After solving for \textbf{x} (i.e. the unknown coefficients, an), the value of [math]\phi[/math] is determined using Equation (Template:EquationNote).
The Method of Moments (MoM) can be used to solve a wide range of equations involving linear operations including integral and differential equations. This numerical technique has many applications other than electromagnetic modeling; however the MoM is widely used to solve equations derived from Maxwell's equations. In general, moment method codes generate and solve large, dense matrix equations and most of the computational resources required are devoted to filling and solving this matrix equation. The particular form of the equations that is solved and the choice of basis and weighting functions have a great impact on the size of this matrix and ultimately the suitability of a given moment method code to model a given geometry.