Homework Assignment
|
Analysis of Magnetic Valve | |
|
Instructor
|
Teaching Assistants:
|
Aim of Assignment
Students will learn the basics of electromagnetic field calculations, their main steps, and gain practice in evaluating results and writing a Technical Report that meets international expectations.
Knowledge needed to solve the problem
- The main steps of the finite element method;
- Theoretical knowledge of the static magnetic field (for defining materials, for excitation);
- Knowledge of CAD system to create geometry;
- Download and install ANSYS AIM Student.
The Semester Assignment
The task consists of two parts, a basic task, with a faultless solution of up to 70%, and an extra task, with an additional maximum of 30%.
| Deadline | May 25, 2019, 12:00 |
| Output Form: | PDF format. Color drawings should be made so that their contents are clear to the reader in black and white. |
| Language | English |
| Place of submission: | marcsa@maxwell.sze.hu email address |
| Late submission: | After every day started, a 5% deduction from the achieved result (i.e. after 5 days delay 100% can only be obtained up to 100% - 5x5% = 75%). |
| Evaluation: | 0 - 50% - Insufficient (1) |
| 51 - 60% - Satisfactory (2) | |
| 61 - 70% Medium (3) | |
| 71 - 85% Good (4) | |
| 86 - 100% - Excellent (5) | |
| For the formal requirements, the requirements of CFD and mechanics are also valid here. | |
Part I of the Assignment
Calculating the force on the solenoid valve by finite element method
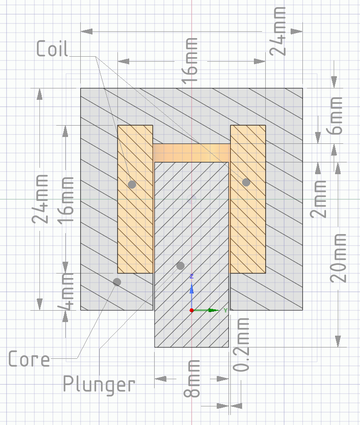
The task is cylindrical to the vertical ([math]z[/math]) axis, and the three-dimensional geometry must be prepared according to the specified dimensions (see figure).
Tasks
- Define the problem type based on the given parameters;
- Creating and specifying the task geometry in ANSYS Discovery AIM;
- Run the FEM simulation;
- Validation of results for a 2mm air gap. The value of the force acting on the plunger: [math]F(z=2\text{mm})=1.4611~\text{N}[/math] (inductance[math]L(z=2\text{mm}=21,27~\text{mH}[/math]);
- Test of Solution Performance (Solution performance tuning, Curved surface meshing) as a function of force;
- Number of finite elements (Tetrahedra), Energy (Total Energy), Energy Error and Delta Energy in the function of adaptive steps in two different cases;
- Postprocessing [at least two of the below]:
- 1) determination of force and inductance;
- 2) displaying equipotential lines;
- 3) display the minimum and maximum of the magnetic flux density;
- 4) display the magnetic field strength;
- 5) displaying magnetic flux density vectors.
- Preparation of a Technical Report based on the use of the above results.
Note: The “Part I of the Assignment” elements will be reviewed in detail during the exercise to prepare and run a simulation model for an electromagnetic task. On this basis, students can easily complete Part I of the Assignment by attending the exercises.
- Parameters for this Assignment:
- Relative permeability of air and coil [math]\mu_r = 1[/math];
- The excitation of the coil (To validate the results): [math]I=0.76~\text{A}[/math], [math]N=789~{turns}[/math] (DC);
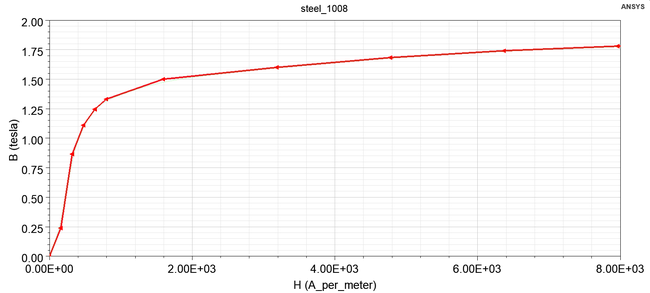
- Magnetic curve of the core and plunge:
- 'Figure 1.' - Steel 1008 steel magnetization curve. Part II. of the Assignment
Determining the force acting on the moving part of the problem (plunger) and the inductance of the coil as a function of displacement.
Note: This task corresponds to the solenoid valve in internal combustion engines that controls the injection.
- Specific tasks
- Considering the plunger movement to the initial state (2mm air gap) from [math]-1.8\text{mm} \text{to} 10\text{mm}[/math] (at least in 7 positions). Detailed instructions on the solution will not be available.
- This part is intended to measure the degree of autonomy, initiative and diligence of the student, i.e.:
- # is the student able to do independent work;
- # to design, assemble and run the simulation alone.