Csőtápvonal
|
Négyszög keresztmetszetű csőtápvonal (Rectangular waveguide) | |
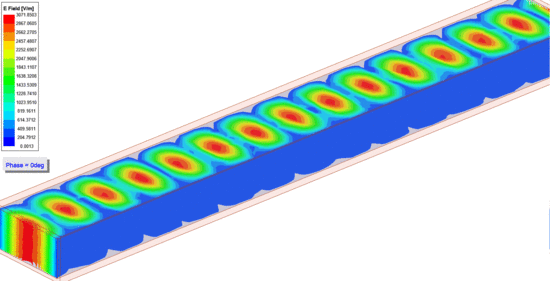
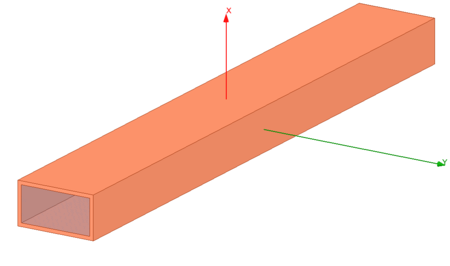
| Négyszög keresztmetszetű csőtápvonal. | Az elektromos térerősség terjedése a csőtápvonalban. [Kattints a képre az animáció megtekintéséhez.] |
|
| |
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása egy négyszög keresztmetszetű csőtápvonal esetében. A szimuláció beállításai és eredményei elősegítsék a más tárgyakból tanult elméleti ismeretek elmélyülését.
A feladat megoldása során azzal nem foglalkozunk, milyen módon lehet a csőtápvonalba jelet juttatni.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A Maxwell-egyenletek teljes rendszerének ismerete (hullámegyenlet ismerete);
- Csőtápvonal működésének ismeret.
A vizsgált csőtápvonal
A feladat geometriai méretei: [math]a = 2\text{cm}[/math] (széles oldal); [math]b = 1\text{cm}[/math] (keskeny oldal); [math]L = 16\text{cm}; th = 1\text{mm}[/math] (csőtápvonal falvastagsága).
A geometria elkészítését és a beállításokat a feladathoz készült YouTube videóban részletezem.
Azonban egy csőtápvonal szimulációja előtt érdemes meghatározni a vágási frekvenciát (vagy határfrekvenciát, ami alatt nincs hullámterjedés a csőtápvonalban). A vágási frekvencia a következő összefüggéssel határozható meg:
- [math] f_{h,mn} = \frac{1}{2\sqrt{\mu\varepsilon}}\sqrt{\left(\frac{m}{a}\right)^2 + \left(\frac{n}{b}\right)^2}[/math],
ahol [math]\mu[/math] és [math]\varepsilon[/math] a csőtápvonalat kitöltő dielektrikum permeabilitása és permittivitása.
A levegővel kitöltött csőtápvonalnál [math]TE_{10}[/math] (ejtsd: té e egy nulla) módus esetében a vágási frekvencia
- [math] f_{h,10} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}}\sqrt{\left(\frac{1}{0.02}\right)^2 + \left(\frac{0}{0.01}\right)^2} = \frac{1}{2\sqrt{\mu_0\varepsilon_0}\cdot0,02}= 7,4926\text{GHz} \approx 7,5\text{GHz}[/math].
A szimulációval kapott eredmények
Ebben az esetben az egész feladat beállításai már előre definiáltak. Ennek oka, hogy elkerüljük a hosszadalmas beállítást, mert a példa fő célja látni egy nagyfrekvenciás kábel hatását a jármű karosszériájára. Ennek a példának köszönhetően, a hallgatók látni fogják, milyen fontos egy kábel vagy kábelkorbács megfelelő elhelyezése a járművön belül. Itt csak a szimuláció felépítését tekintjük át.
A feladat három részre bontható:
- A kábel vizsgálata (ANSYS 2D Extractor);
- A kábel áramkörének összeállítása (ANSYS Circuit);
- és a karosszéria rádiófrekvenciás vizsgálata a benne elhelyezett kábellel együtt (ANSYS HFSS).
A szimuláció elindítása előtt és a futtatás közben, röviden átnézzük a feladat beállításait.
Azt fontos megjegyezni, hogy az első két példánál adaptív hálófinomítást alkalmaztunk. Azonban az időfüggő feladatoknál ez nem lehetséges, ezért itt is a hálózási műveletekkel kell megfelelő felbontást létrehozni a kellő pontosság eléréséhez.
A kábel parazita jelenségeinek vizsgálata (ANSYS 2D Extractor)
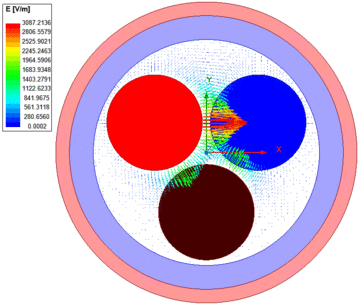
ANSYS 2D Extractor segítségével egy harmonikus analízist futtatunk le (ANSYS Q3D Extractor való a 3D-s feladatokra), hogy meghatározzuk az RLGC paramétereit (R - ellenállás, L - induktivitás, G - átvezetés, C - kapacitás) ennek a csatolt rendszernek.
Ahogy az ábrán látható, a kábel három érből áll, egy pozitív, egy negatív érből és a földelésből. Az egyes erek szigetelve vannak egymástól.
A kábelen haladó jel frekvenciája 300 MHz, a szimulációval kapott eredményeket pedig a következő táblázatok foglalják össze.
|
| ||||||||||||||||||
|
|
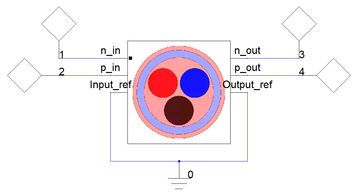
A kábelt meghajtó áramkör (ANSYS Circuit)
A földelést, ahogy a neve is mutatja földeljük, míg a másik két eret 50[math]\Omega[/math] impedanciával zárjuk le. Az ANSYS Circuit a kábel leírására a 2D Extractor szimulációból kapott parazita jellemzőket használja. Majd az áramköri szimulációval kapott eredményeket használja az ANSYS HFSS a szimuláció gerjesztéséhez.
A karosszéria a kábellel (ANSYS HFSS)
ANSYS HFSS (High Frequency Structure Simulator) egy háromdimenziós elektromágneses szimulációs szoftver, a legkülönfélébb rádiófrekvenciás eszközök (antennák, radarrendszerek, kommunikációs rendszerekben található nagysebességű elektronikák, vezetést segítő rendszerek (ADAS), műholdak, integrált áramkörök és IoT eszközök) szimulációjára alkalmas.
A vizsgált példa egy nyitott feladatnak tekinthető, ezért a sugárzási permfeltételt (Radiation boundary condition) használjuk a külső felületeken. Majd erre az elrendezésre oldjuk meg a hullámegyenletet. A feladaton belül a jármű karosszériáját véges vezetőképességgel rendelkező felületként vesszük figyelembe és a gerjesztés a kábelből származó beeső tér.
A szimuláció eredményeként a karosszériában és a kábelen látható az elektromos és a mágneses térerősség. Mindkettő mennyiség jól mutatja a nagyfrekvenciás kábel hatását a járműben.