Lecture 4.
|
Lecture 2. | |
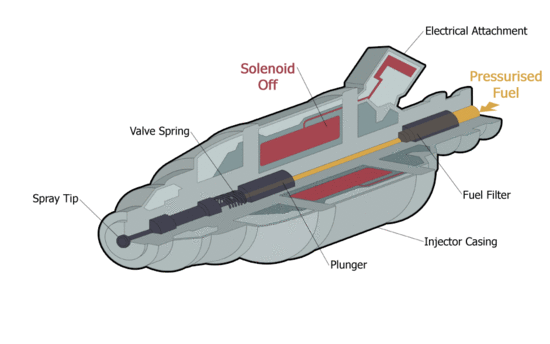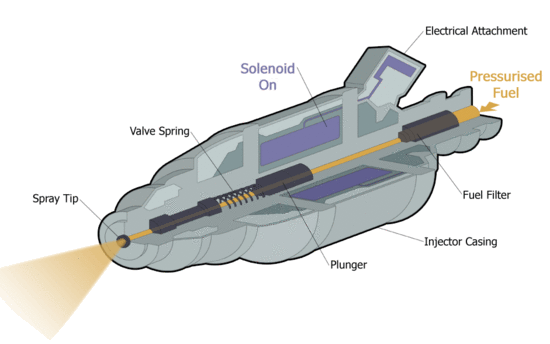
| Animated cut through diagram of a typical fuel injector [1] | Animated cut through diagram of a typical fuel injector [Click to see animation]. |
|
Oktató
|
További oktatók:
|
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása az üzemanyag befecskendező szolenoidjának szimulációján keresztül.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A sztatikus mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- A geometria elkészítéséhez CAD rendszer ismerete.
Finite Element Method (FEM)[2]
Scalar finite element methods have been used by civil and mechanical engineers to analyze material and structural problems since the 1940s. However, it wasn't until the 1960s that FEM codes were developed to solve problems in electromagnetics. Some of the pioneers in this field were Silvester, Zienkiewicz, and Wexler. Initial FEM-based CEM modeling codes were applied to problems in electrostatics and magnetostatics. Later they were used to solve high-frequency problems in 2 dimensions. Practical 3-dimensional codes did not appear until the 1980s due largely to problems with vector parasites and unreliable absorbing boundary conditions. Unwanted reflections from absorbing boundaries continue to be a problem with full-wave 3D FEM codes even today.
Like BEM techniques, finite element methods can be based on different formulations (even the method of moments). However, BEM techniques always solve an integral equation and FEM techniques always solve a differential equation. Every FEM code divides the entire problem domain into small elements. For 2D problems, the elements are usually triangles or rectangles. For 3D problems, the elements are usually tetrahedra (4 faces) or bricks (6 faces). The domain must be finite and bounded. Modeling an unbounded (e.g. radiation) problem requires that the problem domain be bounded with special elements that absorb all incident energy. These elements are called ABC (Absorbing Boundary Condition) elements.
The unknowns in scalar FEM codes are the three orthogonal components of the field at the "nodes" (vertices) of each element. The unknowns in vector FEM codes are the field components along the edges of each element. Scalar codes are conceptually simpler, but they are unsuitable for full-wave modeling, because they are susceptible to spurious solutions that can cause significant and unpredictable errors in the solution. Vector FEM codes are much less likely to exhibit these parasitics.
To form a linear system of equations, the governing differential equation and associated boundary conditions are converted to an integro-differential form using either a variational method or a weighted-residual (moment) method. Variational methods solve for the unknown quantity by minimizing an energy functional. Weighted-residual methods multiply a weak form of Maxwell's equations by a weighting function and integrate over each element. Ultimately, a matrix equation is generated in the form,
[math]\textbf{A}\textbf{x}=\textbf{b}[/math]
where [math]\textbf{x}[/math] is a vector of the unknown field quantities, [math]\textbf{b}[/math] is a vector of source terms, and [math]\textbf{A}[/math] is a sparse matrix whose only non-zero values correspond to positions in the matrix corresponding to edges that share an element.
Generally, the matrices generated by FEM codes are must larger than the matrices generated by BEM codes applied to similar geometries. This is because gridding an entire problem volume requires many more elements than gridding just the material interfaces. However, because FEM matrices are very sparse, they do not necessarily require more storage or computing resources to solve than the small, but dense, matrices generated by BEM codes.
As indicated previously, modeling unbounded problems require special absorbing elements (ABCs). Many formulations of these elements have been proposed. The ABCs that have been developed for 2D FEM codes work very well; however, 3D FEM ABCs work well only at prescribed angles of incidence resulting in the need to locate the boundaries sufficiently far from other structures. Hybrid FEM/BEM codes terminate open surfaces of the FEM volume with a BEM surface negating the need for ABCs. Unfortunately, the BEM portion of the resulting matrix is dense, which can significantly increase the amount of computational resources required.
Perhaps the most attractive feature of the finite element method is its ability to model configurations that have complicated geometries and incorporate various materials. The electrical properties of each element are defined independently and elements can be as small or as large as needed to facilitate the analysis.
The following table summarize various strengths and weakness of FEM modeling techniques. Note that the capabilities of any particular modeling software depend on the specific formulation, the matrix solver and any optimization techniques employed.
Strengths Weaknesses
- Excels at modeling inhomogeneous or complex materials
- Excels at modeling problems that combine small detailed geometries with larger objects
- Excels at modeling structures in resonant cavities or waveguides
- Absorbing boundary required for modeling unbounded (radiation) problems
- Difficult to model thin/electrically large or resonant wires accurately