Homework Assignment
|
Analysis of Solenoid Valve | ||
|
Instructor
|
Teaching Assistants:
| |
Aim of Assignment
Students will learn the basics of electromagnetic field calculations, their main steps, and gain practice in evaluating results and writing a Technical Report that meets international expectations.
Knowledge needed to solve the problem
- The main steps of the finite element method;
- Theoretical knowledge of the static magnetic field (for defining materials, for excitation);
- Knowledge of CAD system to create geometry;
- Download and install Agros2D or FEMM.
The Semester Assignment
The task consists of two parts, a basic task, with a faultless solution of up to 70%, and an extra task, with an additional maximum of 30%.
Deadline May 11, 2020, 23:59 Output Form: PDF format. Color drawings should be made so that their contents are clear to the reader in black and white. Language English Place of submission: In Moodle system. Late submission: After every day started, a 5% deduction from the achieved result (i.e. after 5 days delay 100% can only be obtained up to 100% - 5x5% = 75%). Evaluation: 0 - 48% - Insufficient [F] (1) 50 - 59% - Sufficient [D] (2) 60 - 70% Satisfactory [C] (3) 71 - 84% Good [B] (4) 85 - 100% - Very good [A] (5) For the formal requirements, the requirements of CFD and mechanics are also valid here.
Part I of the Assignment
Calculating the force on the solenoid valve by finite element method
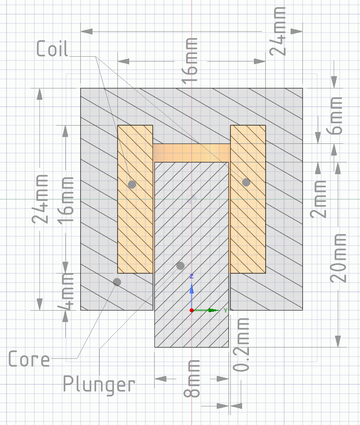
The task is cylindrical to the vertical ([math]z[/math]) axis and the three-dimensional geometry must be prepared according to the specified dimensions (see figure).
Tasks
- Define the problem type based on the given parameters;
- Creating and specifying the task geometry in Agros2D(2D) or FEMM(2D);
- Run the FEM simulation;
- Validation of results for a 2mm air gap.
The results of the simulations. Software Discovery AIM Maxwell 3D FEMM Maxwell 2D Force [N] 3,586 3,582 3,542 3,587 Inductance [mH] 39,88 39,84 39,71 39,84
- Test of the surrounding region's size as a function of force;
- Energy, force, inductance in the function of the number of finite elements (Triangle);
- Postprocessing [at least two of the below]:
- 1) determination of force and inductance;
- 2) displaying equipotential lines;
- 3) display the minimum and maximum of the magnetic flux density;
- 4) display the magnetic field strength;
- 5) displaying magnetic flux density vectors.
- Preparation of a Technical Report based on the use of the above results.
Note: The “Part I of the Assignment” elements will be reviewed in detail during the exercise to prepare and run a simulation model for an electromagnetic task. On this basis, students can easily complete Part I of the Assignment by attending the exercises.
- Parameters for this Assignment:
- Relative permeability of air and coil [math]\mu_r = 1[/math];
- The excitation of the coil (To validate the results): [math]I=0.76~\text{A}[/math], [math]N=789~\text{turns}[/math] (DC);
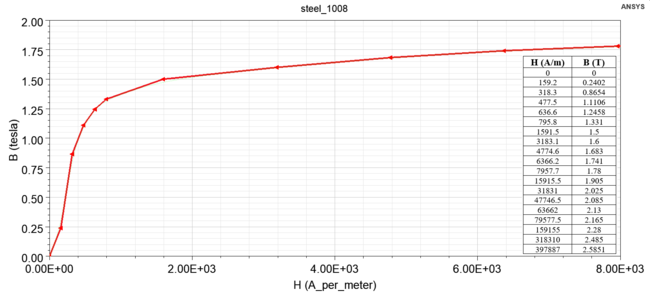
- Magnetic curve of the core and plunge:
Figure 1. - Steel 1008 steel magnetization curve. Part II of the Assignment
Determining the force acting on the moving part of the problem (plunger) and the inductance of the coil as a function of displacement.
Note: This task corresponds to the solenoid valve in internal combustion engines that controls the injection.
- Specific tasks
- Considering the plunger movement to the initial state (2mm air gap) from [math]-1.8\text{mm} \text{ to } 10\text{mm}[/math] (at least in 7 positions). Detailed instructions on the solution will not be available.
- This part is intended to measure the degree of autonomy, initiative and diligence of the student, i.e.:
- is the student able to do independent work;
- to design, assemble and run the simulation alone.
References