Homework Assignment

Analysis of Shunt Resistor
Instructor Dániel Marcsa (lecturer) Lectures: - Office hours: by request	Teaching Assistants: - Office hours: -.

Aim of Assignment

Students will learn the basics of electromagnetic field calculations, their main steps, and gain practice in evaluating results and writing a Technical Report that meets international expectations.

Knowledge needed to solve the problem

• The main steps of the finite element method;
• Theoretical knowledge of the static magnetic field (for defining materials, for excitation);
• Knowledge of CAD system to create geometry;
• Download and install Ansys Electronics Desktop Student.

The Semester Assignment

The task consists of two parts, a basic task, with a faultless solution of up to 70%, and an extra task, with an additional maximum of 30%.

Deadline	-
Output Form:	PDF format. Color drawings should be made so that their contents are clear to the reader in black and white.
Language	English
Place of submission:	In Moodle system.
Late submission:	After every day started, a 5% deduction from the achieved result (i.e. after 5 days delay 100% can only be obtained up to 100% - 5x5% = 75%).
Evaluation:	0 - 48% - Insufficient [F] (1)
	50 - 59% - Sufficient [D] (2)
	60 - 70% Satisfactory [C] (3)
	71 - 84% Good [B] (4)
	85 - 100% - Very good [A] (5)
For the formal requirements, the requirements of CFD and mechanics are also valid here.

Part I of the Assignment

Calculating the resistance and the total loss of the shunt resistor by finite element method

The geometry and dimensions of the task.

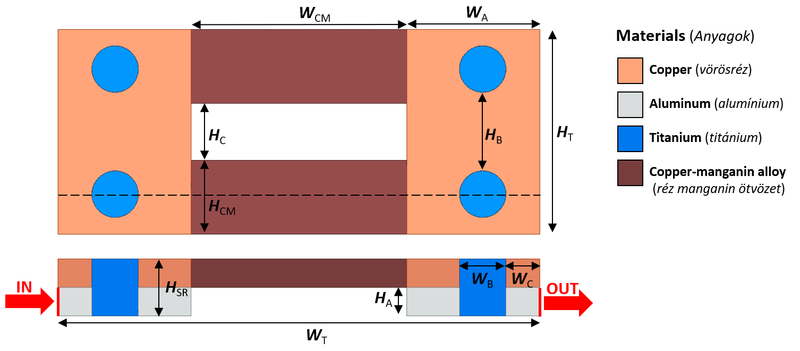
The geometry dimensions for your task you can find in the following table: Semester Assigment.

This task is a DC current conduction problem. The solved equation is

[math]\nabla\cdot\sigma\nabla \varphi=0[/math]

with following boundary conditions

[math]\vec{J}\cdot\vec{n}=-J_{\text{n}}[/math] on [math]\Gamma_{\text{J}}[/math] (This is the input)

and

[math]\varphi=U_0 = \text{0 V}[/math] on [math]\Gamma_{\text{E}}[/math] (This is the output),

where [math]J_{\text{n}}[/math] is the current density calculated from the specified current excitation.

The task: determine the voltage drop, the resistance and the ohmic loss of the problem.
The voltage drop is the potential difference between the two terminals of the arrangement. You can determine resistance using Ohm's law:

[math]R = \frac{U}{I}[/math],

then the ohmic loss

[math]P = I^2\cdot R[/math]

where [math]U[/math] is the voltage drop, [math]I[/math] is the current and [math]R[/math] is the resistance.

Properties of materials.

Material	Titanium	Copper	Aluminum	Copper-manganin alloy
[math]\sigma~[\text{MS/m}][/math]	1.82	58	38	20.833
[math]\rho~[\text{kg}/\text{m}^3][/math]	4500	8933	2689	8400
[math]c_{\text{P}}~[\text{J}/(\text{kg}\cdot\text{°C})][/math]	522	385	951	410
[math]\lambda~[\text{W}/(\text{m}\cdot\text{°C})][/math]	21	400	237.5	22

Tasks

• Draw the geometry based on the specified dimensions.
• Define the problem based on the given material parameters and boundary conditions;
• Creating and specifying the task geometry in Ansys Electronics Desktop Student;
• Run the FEM simulation;

The parameters listed in the task can be calculated with the Maxwell 3D - DC Conduction solver and the Q3D Extractor - DC solver.

Figure 2. - Possible solution (Left - Maxwell 3D, Right - Q3D Extractor).

Results of the test example.

Quantities	Voltage drop [mV]	Resistance [[math]\text{n}\Omega[/math]]	Ohmic loss [W]
Maxwell 3D	10.9927	18.3211	6.5958
Q3D Extractor	10.9759	18.2931	6.5861

Part II of the Assignment

Determining the force acting on the moving part of the problem (plunger) and the inductance of the coil as a function of displacement.

Note: This task corresponds to the solenoid valve in internal combustion engines that controls the injection.

Specific tasks

• Considering the plunger movement to the initial state (2mm air gap) from [math]-1.8\text{mm} \text{ to } 10\text{mm}[/math] (at least in 7 positions). Detailed instructions on the solution will not be available.
• This part is intended to measure the degree of autonomy, initiative and diligence of the student, i.e.:
  1. is the student able to do independent work;
  2. to design, assemble and run the simulation alone.