1. lecke példája
|
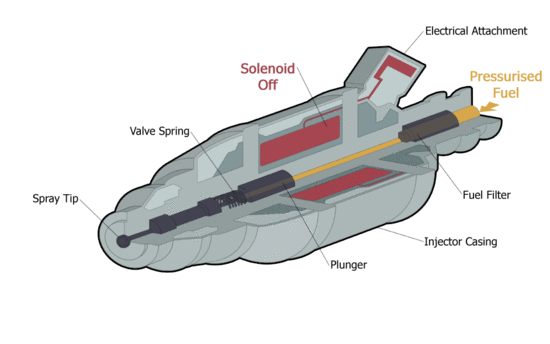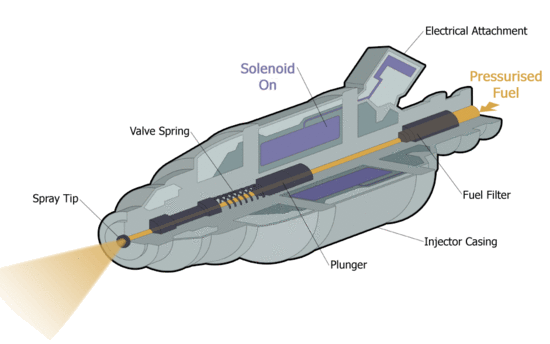
Üzemanyag befecskendező mágnesszelep | |
| Az üzemanyag befecskendező működés közben. [1] | Az üzemanyag befecskendezőnél a B vektorok a szolenoid bekapcsolását követően. |
|
Oktató
|
További oktatók:
|
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása az üzemanyag befecskendező szolenoidjának szimulációján keresztül.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- A sztatikus mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- A geometria elkészítéséhez CAD rendszer ismerete.
A feladat megoldásának lépései
Az ANSYS AIM elindítását követően kiválasztjuk az elektromágneses (Electromagnetics) feladatot a Start gombra kattintva.
A következőkben bemutatott lépésektől eltérően is megvalósítható a feladat. Az AIM használata során a feladat elkészítésében segítséget nyújtanak a különböző lépések során megjelenő üzenetek.
A geometria elkészítése
A feladat geometriáját SpaceClaim-ben, de akár más CAD szoftver segítségével (AutoCAD; SolidWorks; Solid Edge; Catia; Creo; ...) is elkészíthető. A geometria három részből áll, a vasmagból, a stekercsből és a tekercs keresztmetszetéből a gerjesztés megadásához.
A hengeralakú vasmag méretei 14mm maga és 3,6mm a sugara. A tekercs méretei: 20mm magas, 4mm a belső sugár és 14mm a külső sugár.
Geometria elkészítése SpaceClaim-ben
A SpaceClaim megfelelő használatához a Help menüje és a YouTube-on található videók nagy segítséget jelentenek. Itt csak a tekercs keresztmetszetének elkészítését részletezem. Az előadáson és hozzá kapcsolódó gyakorlaton bemutatásra kerül a teljes feladat elkészítése.
Először egy síkor hozunk létre a tekercs-vasmag elrendezés keresztmetszetében a Design - Plane ikon segítségével. Ezt követően a baloldalon található Szerkezet (Structure) ablakban a Tervkomponensre (struktúra fa gyökérébe) kattintva hozzáadunk egy új komponenst (new component). Az új komponens tulajdonságai között (új komponensre kattintva Tulajdonságok (Properties)) a Topológia megosztása (Shared Topology) legyen Megosztásra (Shared) állítva. Ha ezt megtettük, a tekercset húzzuk bele az új komponensbe. Majd a következő lépésként rajzoljuk meg a tekercs keresztmetszetét felhasználva az elrendezés metszeti nézetét. Ha megrajzoltuk a tekercs keresztmetszetét, annak is az új komponens fájában kell lennie. Ennek köszönhetően az ANSYS Discovery AIM a megrajzolt felületet a tekercs keresztmetszeteként fogja kezelni, így erre a felületre előírható a gerjesztés. Végül a
A feladat definiálása
Az anyagokat az egyes térfogatok kiválasztásával tudjuk definiálni.
A tekercs anyaga réz (Copper), a vasmagé 1008-as acél (Steel 1008). Amennyiben ezeknek valamilyen tuljadonságát (vezetőképesség, B-H görbe) módosítani szeretnénk, azt késöbb megtehetjük az anyagok tulajdonságainál.
Ezt követően a gerjesztést kell definiálni. Ehhez a tekercs keresztmetszetének rajzolt felületet kell kiválasztani, majd az áram erősségét (0,2A) és a menetszámot (2000) kell megadni. Itt definálható a tekercs kitöltési tényezője is.
Ha ezzel is megvagyunk, a diszkretizálással és a megoldó beállítasaival nincs teendő, az alapbeállítások megfelelőek lesznek, futtatható a feladat. Adaptív hálózás történik a megoldás során, ezért nem foglalkozunk ennél a feladatnál a végeselemháló beállításával.
Az eredmények kiértékelése
A különböző térváltozók felületre / térfogatba való kirajzoltatásán túl itt tudjuk megnézni a vasmagra ható erő értékét és a tekercs induktivitását.