2. lecke

A végeselem-módszer alapjai / Harmonikus mágneses tér
Oktató Marcsa Dániel (óraadó) Előadás: - Fogadóóra: egyeztetés alapján	További oktatók: - Fogadóóra: -.

Végeselem-módszer (FEM)

A csomóponti végeselem-módszert építő- és gépészmérnökök már az 1940-es években is használták feladatok megoldására. Azonban egészen az 1960-as évekig nem fejlesztettek végeselem-módszert alkalmazó programot elektromágneses feladat megoldására. Ennek a területnek néhány korai úttörője Silvester, Zienkiewicz és Wexler volt. A kezdeti elektromágneses problémákra készített programokkal elektrosztatika és sztatikus mágneses feladatokat oldottak meg. Később kétdimenziós nagyfrekvenciás feladatok megoldására is használták ezeket a programokat. De egészen az 1980-as évekig a nagyfrekvenciás területen nem készült 3D FEM (Finite Element Method) program, a nagy memóriaigény és a megbízhatatlan elnyelő peremfeltétel (Absorbing Boundary Condition - ABC) miatt. A nemkívánatos reflexiók az elnyelő peremfeltételnél még napjainkban is probléma a rádiófrekvenciás feladatoknál.

A végeselem-módszer különböző formalizmusokon alapul ([math]\vec{A},V - \vec{A};\,\vec{T},\phi - \phi[/math]; ...) és mindig differenciálegyenletet old meg. Minden végeselem-módszeren alapuló program a teljes feladathoz tartozó tartományt egyszerű alakzatokra bontja fel. Kétdimenzióban háromszögek vagy négyszögek, háromdimenzióban tetraéder (4 felület) vagy téglatest (6 felület) elemeket használnak (ezen elemek kombinációja is lehet). Általában a feladatnak végesnek és jól körülhatároltnak kell lennie. Olyan esetben, amikor nem körülhatárolható (például sugárzási feladatoknál) speciális elemeket kell alkalmazni, ami elnyeli az összes beeső energiát. Ezeket az elemeket ABC (Absorbing Boundary Condition) elemeknek nevezzük.

A skalár (mértékkel el nem látott) végeselem-módszernél az ismeretlen a három egymásra merőleges összetevője a térváltozónak (vagy valamilyen bevezetett potenciálnak) az összes végeselem csomópontjában (csúcsok). A vektor (mértékkel ellátott) végeselem-módszer esetében az ismeretlenek a végeselemek élein vannak. A skalár FEM egyszerűbb, azonban nem alkalmas a nagyfrekvenciás feladatokra, mert nagyon érzékeny a lokális hibákra, ami jelentős és előre nem látható hibát eredményez a feladat megoldásban. A vektor FEM kevésbé érzékeny, ezért hatékonyabban kezeli a nagyfrekvenciás feladatokat.

Ahhoz, hogy egy lineáris (vagy linearizált) egyenletrendszert kapjunk, a differenciálegyenleteket (Maxwell-egyenletek) és a kapcsolódó peremfeltételeket átalakítjuk integro-differenciális alakra a variációs módszer vagy a súlyozott maradék elvének felhasználásával. A variációs módszer esetében egy energia funkcionál minimalizálásával kapjuk a megoldást. A súlyozott maradék esetében a Maxwell-egyenletek gyenge alakját egy súlyfüggvénnyel szorozzuk és ezt integráljuk minden végeselemre. Végül a következő mátrixegyenletet kell megoldani,

[math]\textbf{A}\textbf{x}=\textbf{b}[/math]

ahol [math]\textbf{x}[/math] az ismeretleneket tartalmazó vektor, [math]\textbf{b}[/math] a gerjesztéseket tartalmazó vektor, and [math]\textbf{A}[/math] a ritka együttható mátrix.

Általában, a végeselem-módszernél sokkal nagyobbak a mátrixok, mint a peremelem-módszernél (Boundary Element Method - BEM) ugyanarra a feladatra. Ennek oka, hogy sokkal több elemet eredményez ha felbontjuk a teljes feladatot, mintha csak az anyagok határait. Azonban mivel a FEM mátrix ritka mátrix, ezért nem biztos, hogy több memóriára vagy számítási kapacitásra van szükség, mint a BEM esetében, ahol sűrű mátrixszal kell dolgozni.

Amint azt korábban írtam, a nem körülhatárolt problémák modellezéséhez speciális elnyelő elemek szükségesek (ABC). Az ABC elemeknek nagyon sok fajtája létezik. A 2D feladatokhoz nagyon jól működnek az ABC peremfeltételek; de háromdimenzióban az elnyelő perem elemei csak adott feltételek között működnek megfelelően, ami azt jelenti, hogy feladattól függő melyik fajta alkalmazható. A hibrid FEM / BEM módszer a végeselemekkel diszkretizált részt BEM-felülettel zárják le, ami miatt nincs szükség elnyelő peremfeltételre. De a kapott mátrix BEM része sűrű, ami jelentősen növelheti a szükséges számítási erőforrást.

A végeselem-módszer egyik legnagyobb előnye, hogy képes a bonyolult geometriák kezelésére és az összetett anyagjellemzők figyelembevételére. Az egyes végeselemek anyagtulajdonságai egymástól eltérőek is lehetnek, mivel függetlenek egymástól, és ezek az elemek tetszőlegesen kicsik vagy nagyon is lehetnek a geometriától függően.

Az alábbi táblázat összefoglalja a végeselem-módszer a főbb erősségeit és gyengeségeit. Fontos megjegyezni, hogy egy adott szoftver képességei nagyon sok mindentől függ, mint az alkalmazott formalizmus, a rendelkezésre álló algebrai egyenletrendszermegoldók vagy a diszkretizálást végző algoritmusok.

Erősségek	Gyengeségek
Kiváló inhomogén és összetett anyagok modellezésére; Kiváló olyan feladatok kezelésére, ahol részletesen elkészített kis alkatrészek és nagy testek egyszerre vannak a feladatban; Kiváló csőtápvonalat és üregrezonátort tartalmazó feladatokhoz.	Elnyelő peremfeltételre van szükség nem körülhatárolt (sugárzó) feladatoknál; Nehéz pontosan modellezni vékony/elektromosan nagy vagy rezonáns vezetékeket.

Frekvenciatartománybeli egyenletek és a kapcsolódó jelenségek áttekintése

Frekvenciatartományban, az időtől való függést az [math]e^{j\omega t}[/math] taggal is kifejezhetjük. Emiatt az idő szerinti deriválás [math]\partial/\partial t[/math] helyett mindenhol használhatjuk a [math]j\omega[/math] való szorzást. Így a Maxwell-egyenletek a következő alakban írhatóak,

[math]\nabla\times\vec{H}=\vec{J}+j\omega D[/math]	Ampere-féle gerjesztési törvény,
[math]\nabla\times\vec{E}=-j\omega \vec{B}[/math]	Faraday-féle indukció törvény,
[math]\nabla\cdot\vec{B}=0[/math]	Fluxusmegmaradás-törvénye,
[math]\nabla\cdot\vec{D}=\rho[/math]	Gauss-törvény,
[math]\nabla\cdot\vec{J}=-j\omega \rho[/math]	Kontinuitási egyenlet.

A frekvenciatartománybeli Maxwell-egyenletek az állandósult állapot vizsgálatára használhatóak. A sztatikus terek esete a frekvenciatartománybeli terek egy esetének tekinthető, ha [math]\omega \to 0[/math]. A frekvenciatartománybeli térváltozók csak helytől ([math]\vec{r}[/math]) függnek, és egy komplex fazorként írjuk le a térváltozókat. A térváltozók fazorral történő leírása és az időtartománybeli leírás között a [math]\cos(\omega t)[/math] esetében a kapcsolat

[math]\vec{H}(x,y,z,t) = \Re\{\vec{H}(x,y,z)e^{j\omega t}\}[/math].

Behatolási mélység

A behatolási mélység egy lehetséges mód, hogy a nem nulla vezetőképességű ([math]\sigma[/math]) anyagokat jellemezzük. A behatolási mélységet úgy definiálhatjuk, hogy a veszteséges anyag felületétől mért azon távolság, ahol a tér amplutúdója [math]1/e[/math]-nyira vagy közelítőleg 37%-ra csökken az anyag felületen lévő értékhez képest. A [math]\delta[/math] behatolási mélység egy jól vezető anyag esetében ([math]\sigma/\omega\varepsilon \gg 1[/math]) a következő összefüggéssel közelíthető

[math]\delta = \sqrt{\frac{2}{\omega\mu\sigma}}[/math].

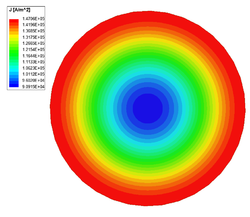
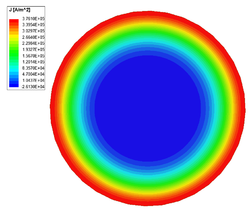
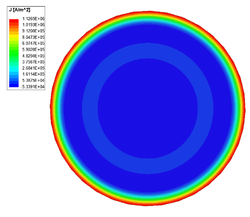
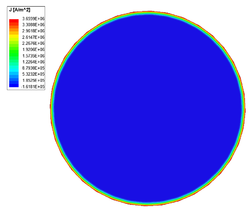
Egy jól vezető anyag esetében a behatolási mélység nagyon kicsi, például nagyfrekvencián azt eredményezi, hogy az áram közelítőleg csak a vezető felületén halad. Az áram kiszorulása csökkenti a vezető hatásos keresztmetszetét (növeli az ellenállását) és növeli a veszteségeket.

Frekvencia [math][\text{Hz}][/math]	Veszteség [math][\text{W}][/math]	Ellenállás [math][\mu\Omega][/math]	Induktivitás [math][\mu\text{H}][/math]
50	0,12677	25,354	0,54144
500	0,32382	67,764	0,51372
5000	0,95942	191,88	0,50105
50000	2,9767	595,34	0,497

Az áramsűrűség a réz vezető keresztmetszetében 50 Hz-en.	Az áramsűrűség a réz vezető keresztmetszetében 500 Hz-en.	Az áramsűrűség a réz vezető keresztmetszetében 5000 Hz-en.	Az áramsűrűség a réz vezető keresztmetszetében 50000 Hz-en.