4. lecke

Integrálegyenleteken alapuló módszerek / Hullámegyenlet
Oktató Marcsa Dániel (óraadó) Előadás: - Fogadóóra: egyeztetés alapján	További oktatók: - Fogadóóra: -.

Integrálegyenleten alapuló módszerek

Peremelem módszer (Boundary Element Method - BEM)

Peremelem módszeren (BEM - Boundary Element Method) alapuló megoldók többsége a momentumok módszerét (MoM - Method of Moments) használja, hogy megoldja az EFIE (Electric Field Integral Equation), az MFIE (Magnetic Field Integral Equation) vagy a CFIE (Combined Field Integral Equation) egyenletrendszert, az elektromos és/vagy mágneses áramokat meghatározásához az egymástól eltérő anyagok közötti határfelületen. Emiatt sok esetben az EM szimulációs programot csak "momentumok módszerén" alapuló szoftverként jellemzik, holott a peremelem módszert használja.

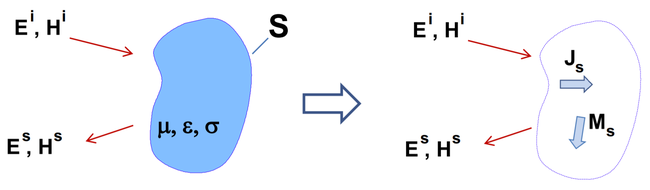
1. ábra - Az egyenértékűség elve.

A peremelem módszer első lépése a probléma geometriájának leírása az azzal egyenértékű felületi áramok eloszlásaként homogén közegben (általában szabad térben). Amint az 1. ábrán látható, az objektum körüli tér az objektumra beeső térből, az objektumról visszavert térből és az objektumból származó térből áll össze. Az egyenértékűségi tétel azt állítja, hogy az objektumon kívüli téreloszlás pontosan leírható, ha eltávolítja az objektumot, és azzal egyenértékű elektromos és mágneses áramokkal helyettesítjük a határfelületen.

Mivel a peremelem módszernél is használt EFIE és MFIE sémák az árameloszlás esetében csak a homogén közegben érvényesek, a feladatban lévő összes objektumot el kell távolítani, és a határaiknak megfelelő (kezdetben ismeretlen) felületi áramokkal kell helyettesíteni.

Az alábbi egyenletek az EFIE és MFIE általános alakját mutatják, ahogy a peremelem módszert használó programok jellemzően alkalmazzák, amelyek csak fémes tárgyakat modelleznek (azaz nincs ekvivalens mágneses felületi áram);

[math]\vec{E}(\vec{r})=\frac{-j\eta}{4\pi k}\int_S\vec{J}_S(\vec{r}')\cdot\vec{G}_e(\vec{r},\vec{r}')\text{d}S'[/math],

[math]\vec{H}(\vec{r})=\frac{1}{4\pi}\int_S\vec{J}_S(\vec{r}')\times\nabla'\vec{G}_m(\vec{r},\vec{r}')\text{d}S'[/math].

Ezekben az egyenletekben a [math]\int_S \text{d}S'[/math] felületre vett integrál az összes határfelületre vett integrálást jelenti. Azt érdemes figyelembe venni, hogy perem csak olyan helyeken létezik, ahol két különböző anyag között határfelület van, tehát a perem mérete korlátozott (azaz nincs integrálás a végtelenbe).

A fenti egyenletekben a [math]\vec{G}_e[/math] és a [math]\vec{G}_m[/math] tagok az elektromos és mágneses teret létrehozó áramokkal kapcsolatos függvények. A [math]\vec{G}_e[/math]-t és [math]\vec{G}_m[/math]-et Green-függvényeknek hívják, és központi szerepet játszanak a peremelem módszerben. A szabadtéri Green-függvény segítségével kifejezhetjük egy külön bázisfüggvénnyel leírt felületi áramok által létrehozott teret (pl.: egy felületdarab árama). Azonban, más Green-függvények is alkalmazhatók egy adott geometriára jellemző, összetettebb szerkezetből származó tér kifejezésére. Például egy vékony dielektrikummal bevont fémfelületekből álló geometriánál alkalmazható egy speciális Green-függvény, amely kifejezi az összevont fém-dielektrikum és dielektrikum-levegő határfelületekből származó teret. Ez jelentősen csökkentheti a probléma modellezéséhez szükséges felületi elemek számát.

Az összes Green-függvény közelíti a megoldást, aminek használhatóságának és pontosságának korlátot szab a frekvencia, a távolság és a geometria. A legtöbb peremelem módszer különböző Green-függvényeket alkalmaz, hogy modellezzék a feladat egyes részeit vagy az eltérő feladatokat.

Az általános célú 3D BEM kódok általában olyan bázis- és súlyfüggvényeket alkalmaznak, amelyek lineáris árameloszlást eredményeznek a háromszög vagy négyszögletes felületdarabokon. Általában két ismeretlen, két ortogonális (egymásra merőleges) áramvektor van felületdarabonként. A vékony vezetékeket hatékonyan leírhatóak egy ismeretlenes elemekkel, ahol az ismeretlen az árameloszlás amplitúdója vezetékdarabonként.

A pont-illesztési eljárásnál a bázis- és súlyfüggvényt Dirac-deltának választjuk, melyek jellemzően a felületelem középpontjában helyezkedik el. Az ugrásfüggvény-illesztési módszernél a bázis- és súlyfüggvényt állandó értéknek vesszük az egész felületelemen. A pontosabb megvalósításnál olyan bázis- és súlyfüggvényt alkalmaznak, amelynél folytonos az átmenet két szomszédos felületelem között. A Rao-Wilton-Glisson (RWG) bázisfüggvény a legelterjedtebben alkalmazott háromszög alakú felületelemeket alkalmazó programoknál. A téglalap alakú elemeket alkalmazó szoftverek jellemzően "háztető" (roof-top) bázisfüggvényt használnak.

Általában azok az elektromágneses szimulációs szoftverek, amelyek a peremelem módszeren alapulnak nagyon jók nyitott feladatok modellezésére, különösen akkor, ha ezen belül nincs szükség a nagyon összetett tartományok részletes modellezésére. A vonalakkal jól leírható szerkezetek nagyon hatékonyan modellezhetőek a peremelem módszerrel.

Az alábbi táblázat összegzi a BEM modellezés erősségeit és gyengeségeit. Fontos megjegyezni, hogy az egyes modellező szoftverek képességei erősen függenek a megoldandó integrált egyenlet formájától, a bázis- és súlyfüggvény megválasztásától, az alkalmazott Green-függvény(ek)től, valamint az egyenletrendszer megoldójától és az alkalmazott optimalizálási technikáktól.

Erősségek	Gyengeségek
Kiváló a sugárzási feladatok modellezésében. Kiváló a fémfelületek és vékony vezetékek modellezésére. Jó a koncentrált paraméterű áramkörrel összekapcsolt szerkezetek modellezésében.	Nem modellezi jól az inhomogén vagy összetett anyagokatat. Nem alkalmas olyan feladatok modellezésére, amelyekben a kis részek mellett nagyobb objektumok is vannak. A rezonáns méretű zárt struktúrák modellezéséhez CFIE formalizmus szükséges.

Momentumok módszere (Method of Moments - MoM)

Már 1960-ban, mások mellett R.F. Harrington is alkalmazott egy momentumok módszerének nevezett eljárást elektromágneses feladatok megoldására. A momentumok módszere egy eljárás, ami a feladatot lineáris egyenletrendszerré képezi le

[math]\mathcal{L}(\phi)=f[/math],

ahol a [math]\mathcal{L}(\bullet)[/math] funkcionál egy lineáris operátor, az [math]f[/math] az ismert gerjesztés vagy kényszer függvénye és a [math]\phi[/math] az ismeretlen mennyiség. Ahhoz, hogy számítógépen kezelhető feladatot kapjunk, a feladatot [math]N[/math] részre (2D - vonal, 3D - felület) felbontjuk, majd az ismeretlen függvényt ugyanennyi súlyozott bázisfüggvény ([math]v_n[/math]) összegeként kell közelíteni,

[math]\phi = \sum_{n=1}^{N}a_n v_n[/math],

ahol [math]a_n[/math] az ismeretlen együttható, ami a sorozat egyes tagjainak az amplitúdóját adja meg.

Ennek következtében, most nem egy egyenletünk van a [math]\phi[/math] ismeretlennel, hanem ehelyett [math]N[/math] darab skalár ismeretlen van,

[math]\mathcal{L}(a_1v_1+a_2v_2+\dots+a_Nv_N)=f[/math].

Ahhoz, hogy meghatározzuk [math]a_n[/math] értékeit, [math]N[/math] darab egymástól lineárisan független egyenletre van szükségünk; amihez [math]a_n[/math] különböző súly- vagy tesztfüggvényeket, [math]w_n[/math]-t alkalmazunk. Ennek következtében [math]N[/math] egyenletből álló egyenletrendszerünk van az [math]N[/math] ismeretlenhez:

[math] \begin{bmatrix} \langle w_1,\mathcal{L}(v_1)\rangle & \langle w_1,\mathcal{L}(v_2)\rangle & \cdots & \langle w_1,\mathcal{L}(v_N)\rangle \\ \langle w_2,\mathcal{L}(v_1)\rangle & \langle w_2,\mathcal{L}(v_2)\rangle & \cdots & \langle w_2,\mathcal{L}(v_N)\rangle \\ \vdots & \ddots & \vdots \\ \langle w_N,\mathcal{L}(v_1)\rangle & \langle w_N,\mathcal{L}(v_2)\rangle & \cdots & \langle w_N,\mathcal{L}(v_N)\rangle \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_N \end{bmatrix} = \begin{bmatrix} \langle w_1, f_1 \rangle \\ \langle w_2, f_2 \rangle \\ \vdots \\ \langle w_N, f_N \rangle \end{bmatrix}. [/math]

A fenti összefüggés lineáris egyenletrendszerként a következő lesz

[math]\textbf{A}\textbf{x}=\textbf{b}[/math],

ahol az [math]\textbf{A}[/math] mátrix elemei ismert értékek, amelyeket a [math]\mathcal{L}(\bullet)[/math] lineáris operátorból és a kiválasztott bázis- és súlyfüggvények segítségével számítható. A \textbf{b} elemeit az ismert gerjesztési függvényből és a súlyfüggvényből lehet meghatározni. A [math]\textbf{x}[/math] vektor ismeretlen elemeit az egyenletrendszer megoldásával kapjuk. Az [math]\textbf{x}[/math] mátrix elemeinek (azaz az ismeretlen együtthatók, [math]a_n[/math]) meghatározása után, a [math]\phi[/math] értékét a [math]\phi = \sum_{n=1}^{N}a_n v_n[/math] egyenlet segítségével számítjuk.

A momentumok módszere (MoM) az egyenletek széles skálájának megoldására alkalmazható, ideértve az integrál- és a differenciálegyenleteket. Ennek a numerikus technikának az elektromágneses modellezésen kívül sok egyéb alkalmazása van, azonban a MoM-ot széles körben a Maxwell-egyenletekből származó egyenletek megoldására használják. Általánosságban elmondható, hogy a MoM-ra épülő megoldók nagy, sűrű mátrix egyenleteket generálnak és oldanak meg, és a szükséges számítási erőforrások nagy részét ennek a mátrix egyenletnek a asszemblálására és megoldására fordítják. A megoldandó egyenletek alakja, valamint az bázis- és a súlyfüggvények megválasztása nagy befolyással bír ennek a mátrixnak a méretére, és végül a MoM megoldó alkalmasságára egy adott geometria modellezésénél.

Elektromos- és mágneses térerősség integrálegyenlet

A momentumok módszerét használó programcsomagok legelterjedtebben az elektromos térerősség integrálegyenletet (Electric Field Integral Equation - EFIE) oldják meg. Ennek az általános alakja

[math]\vec{E}=f_e(\vec{J},\vec{M})[/math],

ahol [math]\vec{E}[/math] a beiktatott (azaz forrás) elektromos térerősség és a [math]\vec{J}[/math] és a [math]\vec{M}[/math] az indukált elektromos és mágneses áramsűrűség. Az EFIE-ről a peremelem módszernél is említést tettünk. Általában az elektromos térerősség integrálegyenletet használó programok kitűnőek a nyitott feladatok modellezésére, ha a forrás közelében (a közelterében) az elektromos térerősség a jelentősebb.

Egy másik egyenlet, amit a momentumok módszere segítségével megoldunk a mágneses térerősség integrálegyenlet (Magnetic Field Integral Equation - MFIE), aminek az általános alakja,

[math]\vec{H}=f_m(\vec{J},\vec{M})[/math],

ahol [math]\vec{H}[/math] a beiktatott (azaz forrás) mágneses térerősség. Az örvényáramú feladatoknál, ahol a mágneses térerősség jelentősebb a közeltérnél a mágneses térerősség integrálegyenletet alkalmazzák a programok.

A csak az EFIE vagy csak az MFIE megoldására épülő momentumok módszere instabillá válhat, amikor a vizsgált felület az adott frekvencián üregrezonátorként viselkedik. Ennek elkerüléséhez a momentumok módszer az EFIE és az MFIE egyenletek lineáris kombinációját, az úgynevezett kombinált térerősség integrálegyenletet (Combined Field Integral Equation - CFIE) oldja meg. Ennél nagyobb számítási kapacitásra van szükség a mátrix feltöltéséhez, de stabilabb megoldást eredményez, ha olyan felületet oldunk meg, ami kellően nagy, hogy belső rezonancia alakuljon ki.

Néhány elektromágneses szimulációs szoftver a momentumok módszerét más egyenletek megoldására használja. Például sztatikus feladatoknál használják a Laplace-egyenletként megfogalmazott problémák megoldására, ahol az elektromos térerősségből a töltéssűrűséget, vagy a mágneses térerősségből az áramsűrűséget számolják. Egy másik példa a Generalized Multipole Technique (GMT), ami a momentumok módszerét használja a többpólusú forrásokkal létrehozott elektromos tér meghatározására.

Bázis- és súlyfüggvény

A bázis- és a súlyfüggvény megfelelő választása óriási különbséget eredményezhet az elfogadható pontosságú megoldáshoz szükséges [math]N[/math] elemek számában. Mivel a megoldást a bázisfüggvények összegzésével kapjuk, fontos olyan bázisfüggvényt választani, amelyek kis szám esetében is pontosan leírja a megoldást. Például, amikor a felületi árameloszlást számoljuk, a bázisfüggvényeknek olyan árameloszlást leíró elemeknek kell lenniük, amelyeket összegezve megfelelően közelítik a feladatban fellépő lehetséges árameloszlásokat.

Súlyfüggvénynek olyan kell választani, ami maximalizálja az egyenlet különböző súlyozott formáinak lineáris függetlenségét. Gyakran a legjobb, ha a bázisfüggvénnyel azonos súlyfüggvényt választunk. A momentumok módszer technikáinál is, ha a bázisfüggvény és a súlyfüggvény azonosak azt Galjorkin-módszernek nevezzük.

Hullámegyenlet

Itt a közvetlenül elektromos és mágneses térből előálló frekvenciatartománybeli egyenletekkel foglalkozunk. Ezeket szintén a Maxwell-egyenletekből kapjuk, amelyek mind az elektromos, mind a mágneses teret tartalmazza, amíg a hullámegyenlet mindig csak az egyik mennyiséget tartalmazza.

Hullámegyenlet

Az [math]\vec{E}[/math] elektromos térerősségre a hullámegyenletet kapjuk, ha kiküszöböljük a [math]\vec{H}[/math] mágneses térerősséget a I. és II. Maxwell-egyenletből a konstitúciós relációk segítségével. Ezt megtéve az elektromos térerősségre a hullámegyenlet

[math]\nabla\times\left(\frac{1}{\mu}\nabla\times\vec{E}\right)-\omega^{2}\varepsilon\vec{E}=-j\omega\vec{J}[/math].

Hasonlóképpen, az [math]\vec{E}[/math] elektromos térerősség kiküszöbölésével a mágneses térerősségre a hullámegyenlet

[math]\nabla\times\left(\frac{1}{\varepsilon}\nabla\times\vec{H}\right)-\omega^{2}\mu\vec{H}=\nabla\times\left(\frac{1}{\varepsilon}\vec{J}\right)[/math].

Ezeket az egyenleteket inhomogén hullámegyenletnek nevezzük. Az [math]\vec{E}[/math]-re kifejezett hullámegyenlet megoldása kielégíti a Gauss-törvényt és ugyanígy a [math]\vec{H}[/math]-ra kifejezett hullámegyenlet megoldása kielégíti a fluxusmegmaradás törvényét.