Difference between revisions of "3. lecke példája"
(→Az eredmények kiértékelése) |
|||
| (17 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
[[File:PMMotor Prius2004.gif|550px]] | [[File:PMMotor Prius2004.gif|550px]] | ||
|- | |- | ||
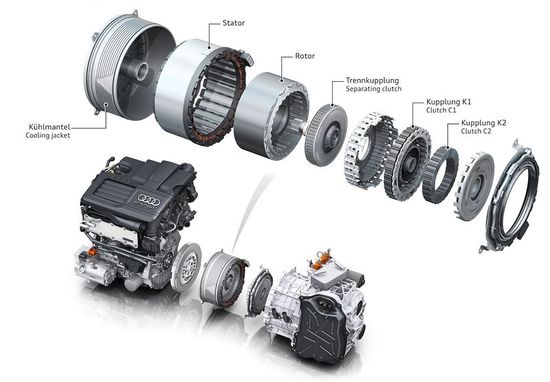
| − | |align=center | Audi A3 Sportback e-tron hajtásláncának meghajtó egysége. | + | |align=center | <span style="font-size:88%;">'''Audi A3 Sportback e-tron hajtásláncának meghajtó egysége.'''</span><ref>Audi Technology Portal - https://www.audi-technology-portal.de/en/mobility-for-the-future/audi-future-lab-tron-experience_en/audi-a3-e-tron_en</ref> |
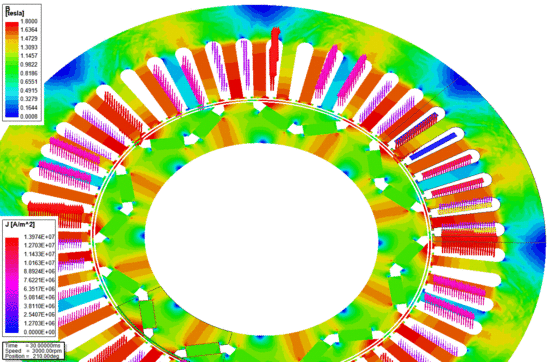
| − | |align=center | Állandó mágneses szinkron motor üzem közben. [Kattints a képre az animáció megtekintéséhez] | + | |align=center | <span style="font-size:88%;">'''Állandó mágneses szinkron motor üzem közben.'''</span> <span style="font-size:80%; color:blue;">[Kattints a képre az animáció megtekintéséhez.]</span> |
|- valign=top | |- valign=top | ||
| width=50% | | | width=50% | | ||
| + | ''' ''' | ||
| + | |- | ||
| + | | style="text-align: left; width: 36%;" | | ||
'''Oktató''' | '''Oktató''' | ||
| − | * Marcsa Dániel (óraadó) | + | * [http://wiki.maxwell.sze.hu/index.php/Marcsa Marcsa Dániel] (óraadó) |
| − | * Előadás: | + | * Előadás: - |
* Fogadóóra: egyeztetés alapján | * Fogadóóra: egyeztetés alapján | ||
| − | | width | + | | style="text-align: left; width: 36%;" | |
'''További oktatók:''' | '''További oktatók:''' | ||
* - | * - | ||
| Line 32: | Line 35: | ||
=== A feladat megoldásának lépései === | === A feladat megoldásának lépései === | ||
| − | Az ANSYS Electronics Desktop elindítását követően a ''File <math>\to</math> Open'' almenü segítségével nyissuk meg a '''PM_Motor_Oktatas.aedt''' fájlt. | + | Az ANSYS Electronics Desktop elindítását követően a ''File <math>\to</math> Open'' almenü segítségével nyissuk meg a '''PM_Motor_Oktatas.aedt''' fájlt. <br/> |
| − | |||
Az ANSYS Maxwell használatához a ''Help'' menüje és a ''YouTube''-on fellelhető videók sok segítséget nyújtanak. | Az ANSYS Maxwell használatához a ''Help'' menüje és a ''YouTube''-on fellelhető videók sok segítséget nyújtanak. | ||
| Line 56: | Line 58: | ||
A példa célja bemutatni a villamos gépek nemkívánatos jelenségeinek forrását. A melegedés forrása a gép különböző részeiben keletkező veszteség. Az örvényáram veszteséggel az előző leckében már találkoztunk. Azonban az úgynevezett [https://en.wikipedia.org/wiki/Electrical_steel elektromos acéloknál] több összetevője van a vasveszteségnek | A példa célja bemutatni a villamos gépek nemkívánatos jelenségeinek forrását. A melegedés forrása a gép különböző részeiben keletkező veszteség. Az örvényáram veszteséggel az előző leckében már találkoztunk. Azonban az úgynevezett [https://en.wikipedia.org/wiki/Electrical_steel elektromos acéloknál] több összetevője van a vasveszteségnek | ||
| − | <math> p_{\text{vas}} = p_{\text{h}} + p_{\text{c}} + p_{\text{e}} = K_{\text{h}}f(B_{\text{max}})^2 + K_{\text{c}}(f B_{\text{max}})^2 + K_{\text{e}}(f B_{\text{max}})^{1.5} </math>, | + | ::<math> p_{\text{vas}} = p_{\text{h}} + p_{\text{c}} + p_{\text{e}} = K_{\text{h}}f(B_{\text{max}})^2 + K_{\text{c}}(f B_{\text{max}})^2 + K_{\text{e}}(f B_{\text{max}})^{1.5} </math>, |
| − | ahol <math>p_{\text{h}}</math> a hiszterézis veszteség, <math>p_{\text{c}}</math> az örvényáram veszteség, <math>p_{\text{e}}</math> a járulékos veszteség, <math>K_{\text{h}}, K_{\text{c}}, K_{\text{e}}</math> a veszteségekhez tartozó együttható, <math>f</math> a frekvencia és <math>B_{\text{ | + | ahol <math>p_{\text{h}}</math> a hiszterézis veszteség (''Hysteresis loss''), <math>p_{\text{c}}</math> az örvényáram veszteség (''Eddy current loss''), <math>p_{\text{e}}</math> a járulékos veszteség (''Excess loss''), <math>K_{\text{h}}, K_{\text{c}}, K_{\text{e}}</math> a veszteségekhez tartozó együttható, <math>f</math> a frekvencia és <math>B_{\text{max}}</math> a mágneses fluxussűrűség maximuma. A ''B. ábra'' a vasveszteséget és az összetevőit mutatja az idő függvényében. |
A másik fő nemkívánatos jelenség a villamos gépeknél a rezgés. A rezgésnek itt csak egy forrásával foglalkozunk, a légrésben kialakuló indukcióval (légrésindukció), amely a gép kialakításától függően eltér a szinusztól, tehát felharmonikustartalommal bír. A Maxwell-féle feszültségtenzor szerint az állórész furatára és a forgórész palástfelületére ható húzóerő (a radiális erő nagysága) a légrésindukció normális összetevőjének négyzetével arányos. A Maxwell-féle feszültségtenzor a következő összefüggéssel számítható | A másik fő nemkívánatos jelenség a villamos gépeknél a rezgés. A rezgésnek itt csak egy forrásával foglalkozunk, a légrésben kialakuló indukcióval (légrésindukció), amely a gép kialakításától függően eltér a szinusztól, tehát felharmonikustartalommal bír. A Maxwell-féle feszültségtenzor szerint az állórész furatára és a forgórész palástfelületére ható húzóerő (a radiális erő nagysága) a légrésindukció normális összetevőjének négyzetével arányos. A Maxwell-féle feszültségtenzor a következő összefüggéssel számítható | ||
| − | <math>\vec{sigma} = \frac{1}{\mu_0}\left(\vec{B}\cdot\vec{n}\right)\vec{B} - \frac{1}{2\mu_0}B^2\vec{n}, | + | ::<math>\vec{\sigma} = \frac{1}{\mu_0}\left(\vec{B}\cdot\vec{n}\right)\vec{B} - \frac{1}{2\mu_0}B^2\vec{n}</math>, |
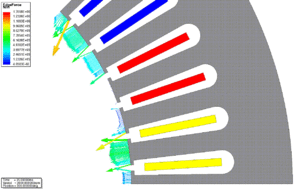
| − | ahol <math>B = |\vec{B}|</math> a mágneses fluxussűrűség abszolút értéke. A ''J. ábra'' a fogerők változását mutatja. | + | ahol <math>B = \|\vec{B}\|</math> a mágneses fluxussűrűség abszolút értéke. A ''J. ábra'' a fogerők változását mutatja. |
{| width=100% | {| width=100% | ||
|- | |- | ||
| Line 74: | Line 76: | ||
[[File:PMMotor EdgeForce.gif|300px]] | [[File:PMMotor EdgeForce.gif|300px]] | ||
|- | |- | ||
| − | |align=center | ''B. ábra'' - A vasveszteség és annak összetevői az idő függvényében. | + | |align=center | <span style="font-size:88%;">''' ''B. ábra'' - A vasveszteség és annak összetevői az idő függvényében.'''</span> |
| − | |align=center | ''K. ábra'' - A relatív permeabilitás az álló- és forgórészben. | + | |align=center | <span style="font-size:88%;">''' ''K. ábra'' - A relatív permeabilitás az álló- és forgórészben.'''</span> |
| − | |align=center | ''J. ábra'' - A fogerő változása az idő függvényében [Kattints a képre az animáció megtekintéséhez] | + | |align=center | <span style="font-size:88%;">''' ''J. ábra'' - A fogerő változása az idő függvényében.'''</span> <span style="font-size:80%; color:blue;">[Kattints a képre az animáció megtekintéséhez.]</span> |
|} | |} | ||
== Irodalomjegyzék == | == Irodalomjegyzék == | ||
{{reflist}} | {{reflist}} | ||
Latest revision as of 20:00, 28 January 2020
|
Állandó mágneses motor | |
| Audi A3 Sportback e-tron hajtásláncának meghajtó egysége.[1] | Állandó mágneses szinkron motor üzem közben. [Kattints a képre az animáció megtekintéséhez.] |
|
| |
|
Oktató
|
További oktatók:
|
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása egy időfüggő szimuláción keresztül. Elősegítse a villamos forgógépekben jelentkező jelenségek - zaj, rezgés, melegedés - forrásának megértését.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- Az időben változó mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- Alapvető ismeretek a villamos gépek működéséről.
A feladat megoldásának lépései
Az ANSYS Electronics Desktop elindítását követően a File [math]\to[/math] Open almenü segítségével nyissuk meg a PM_Motor_Oktatas.aedt fájlt.
Az ANSYS Maxwell használatához a Help menüje és a YouTube-on fellelhető videók sok segítséget nyújtanak.
A feladat definiálása
Ebben az esetben a feladat geometriája és a feladat definiálása előre elkészített. Ennek oka, a hosszadalmas beállítás elkerülése és az, hogy alapvetően a példa azt a célt szolgálja, hogy a nemkívánatos jelenségek forrásait (erő, veszteség) áttekintsük egy villamos forgógép példáján.
A futtatás előtt és közben röviden áttekintjük a feladat beállításait.
Fontos megjegyezni, hogy az előző két példa esetében az adaptív hálozó finomította a felbontást. Azonban időfüggő (tranziens) esetben nincs lehetőség az adaptív hálózó használatára, így nekünk kell előre definiálni a feladat felbontását különböző hálózási műveletekkel.
A megoldó beállítása, a szimuláció futtatása
A megoldónál definiálni kell az időtartomány végét, ameddig futtani szeretnénk a szimulációt, valamint az időlépést. Ennél a példánál 15 ms legyen az időtartomány vége (Stop time) és 0,05 ms (periodusonként 100 időlépés) az időlépés (Time step).
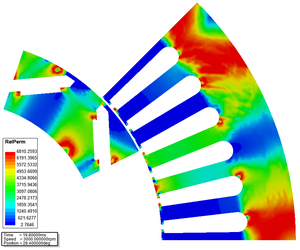
Itt már szükség lehet a nemlineáris megoldó beállításaira is, mivel az állórészt és forgórészt alkotó acél mágnesezési görbéje ([math]\vec{B} - \vec{H}[/math] kapcsolat) nemlineáris. Erre jó példa a lenti K. ábra, ahol látható, hogy milyen nagy mértékben különbözhet helyről-helyre a relatív permeabilitás értéke.
Ahhoz, hogy a szimuláció lefutását követően több időpillanatban megjelenítsük az eredményt, szükség van megadni, melyik időlépésben szeretnénk a megoldást elmenteni. Ha ezt nem tesszük meg, automatikusan az utolsó időlépést menti el, ebben az időpillanatban lehet a térváltozókat ([math]\vec{A}; \vec{B}; \vec{H}[/math]; ...) és az azokból származtatott mennyiségeket ([math]\text{veszteség}, \text{energia}, ...[/math]) megjeleníteni.
Az eredmények kiértékelése
A példa célja bemutatni a villamos gépek nemkívánatos jelenségeinek forrását. A melegedés forrása a gép különböző részeiben keletkező veszteség. Az örvényáram veszteséggel az előző leckében már találkoztunk. Azonban az úgynevezett elektromos acéloknál több összetevője van a vasveszteségnek
- [math] p_{\text{vas}} = p_{\text{h}} + p_{\text{c}} + p_{\text{e}} = K_{\text{h}}f(B_{\text{max}})^2 + K_{\text{c}}(f B_{\text{max}})^2 + K_{\text{e}}(f B_{\text{max}})^{1.5} [/math],
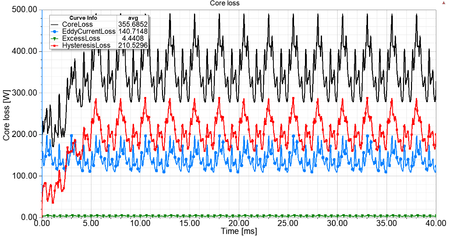
ahol [math]p_{\text{h}}[/math] a hiszterézis veszteség (Hysteresis loss), [math]p_{\text{c}}[/math] az örvényáram veszteség (Eddy current loss), [math]p_{\text{e}}[/math] a járulékos veszteség (Excess loss), [math]K_{\text{h}}, K_{\text{c}}, K_{\text{e}}[/math] a veszteségekhez tartozó együttható, [math]f[/math] a frekvencia és [math]B_{\text{max}}[/math] a mágneses fluxussűrűség maximuma. A B. ábra a vasveszteséget és az összetevőit mutatja az idő függvényében.
A másik fő nemkívánatos jelenség a villamos gépeknél a rezgés. A rezgésnek itt csak egy forrásával foglalkozunk, a légrésben kialakuló indukcióval (légrésindukció), amely a gép kialakításától függően eltér a szinusztól, tehát felharmonikustartalommal bír. A Maxwell-féle feszültségtenzor szerint az állórész furatára és a forgórész palástfelületére ható húzóerő (a radiális erő nagysága) a légrésindukció normális összetevőjének négyzetével arányos. A Maxwell-féle feszültségtenzor a következő összefüggéssel számítható
- [math]\vec{\sigma} = \frac{1}{\mu_0}\left(\vec{B}\cdot\vec{n}\right)\vec{B} - \frac{1}{2\mu_0}B^2\vec{n}[/math],
ahol [math]B = \|\vec{B}\|[/math] a mágneses fluxussűrűség abszolút értéke. A J. ábra a fogerők változását mutatja.
| B. ábra - A vasveszteség és annak összetevői az idő függvényében. | K. ábra - A relatív permeabilitás az álló- és forgórészben. | J. ábra - A fogerő változása az idő függvényében. [Kattints a képre az animáció megtekintéséhez.] |