Difference between revisions of "Feladat 5"

Revision as of 20:43, 24 October 2020 (view source) Marcsa (talk | contribs) (/* A hővezetés differenciálegyenleteSzabó I., Áramlástan, műszaki hőtan, Tankönyvkiadó, Budapest, 1973.Imre L., Villamos gépek és eszözök melegedése és hűtése - 2. Bevezetés a hőátviteli folyamatok elméletébe, Műszaki Könyvkiad...) ← Older edit		Revision as of 20:44, 24 October 2020 (view source) Marcsa (talk | contribs) (/* A hővezetés differenciálegyenleteSzabó I., Áramlástan, műszaki hőtan, Tankönyvkiadó, Budapest, 1973.Imre L., Villamos gépek és eszözök melegedése és hűtése - 2. Bevezetés a hőátviteli folyamatok elméletébe, Műszaki Könyvkiad...) Newer edit →
Line 207:		Line 207:
	amit visszahelyettesítve és átrendezve a következő egyenletre vezet:		amit visszahelyettesítve és átrendezve a következő egyenletre vezet:
−	<math>\text{d}\tau\int_{V} c\cdot\rho\cdot\frac{\partial T}{\partial \tau}~\text{d}V = \text{d}\tau\int_{V} q_V~\text{d}V -\text{d}\tau\int_{V} \nabla\cdot\vec{q}~\text{d}V \rightarrow \text{d}\tau\int_{V} \big(c\cdot\rho\cdot\frac{\partial T}{\partial \tau} - q_V + \nabla\cdot\vec{q}\big)~\text{d}V = 0</math>	+	<math>\text{d}\tau\int_{V} c\cdot\rho\cdot\frac{\partial T}{\partial \tau}~\text{d}V = \text{d}\tau\int_{V} q_V~\text{d}V -\text{d}\tau\int_{V} \nabla\cdot\vec{q}~\text{d}V \rightarrow \text{d}\tau\int_{V} \big(c\cdot\rho\cdot\frac{\partial T}{\partial \tau} - q_V + \nabla\cdot\vec{q}\big)~\text{d}V = 0</math>.
	Figyelembe véve azt, hogy az integrál zérus értéke az integrandusz zérus voltát jelenti, tehát		Figyelembe véve azt, hogy az integrál zérus értéke az integrandusz zérus voltát jelenti, tehát

---

Revision as of 20:44, 24 October 2020

Feladat #5 - Stacionárius hőáramlás Contents  [hide]  1 A feladat célja 2 A feladat megoldásához szükséges ismeretek 3 A feladat 4 Feladat I. része 4.1 Rezisztencia és veszteség számítása végeselem-módszerrel 4.2 Szoftverek használatának bemutatása 4.3 A hővezetés differenciálegyenlete[1][2] 5 Feladat II. része 6 Hivatkozások
Oktató Marcsa Dániel (óraadó) Előadás: - Fogadóóra: egyeztetés alapján	További oktatók: - Fogadóóra: -.

A feladat célja

A hallgatók elsajátítsák az elektromágneses térszámítás alapjait, főbb lépéseit, valamint gyakorlatot szerezzen az eredmények kiértékelésében a FEMM vagy az Agros2D szoftver segítségével. Ezen túl a nemzetközi elvárásoknak megfelelő Műszaki Jelentés (Technical Report) írásában is gyakorlatot szerezzen.

A feladat egy háromfázisú kábel (lásd Feladat 4) egyik vezetőjében kialakuló hőmérsékleteloszlás meghatározása a vezetékben létrejövő veszteség ismeretében.

A feladat megoldásához szükséges ismeretek

• A végeselem-módszer lépései;
• A stacionárius hőáramlásra vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés és peremfeltétel megadásához) [Ebben segítséget nyújt a lenti el elméleti összefoglaló.];
• A FEMM vagy Agros2D szoftver alapszintű kezelése.

A feladat

A feladat két részből áll, a szimulációból és az összefoglaló elkészítéséből.

Leadási határidő:	nappali - 2020. december 5. 23:59 / távoktatás - 2020. december 5. 23:59
Leadás formája:	A szimulációs fájlt (FEMM - *.feh; Agros2D - *.a2d) tömörítve (.zip formátumban). Az összefoglalót PDF formátumban. A színes ábrákat úgy kell elkészíteni, hogy fekete-fehérben kinyomtatva is világos legyen a tartalmuk az olvasó számára.
Benyújtás nyelve:	Magyar
Benyújtás helye:	A Moodle rendszerben kiírt feladatnál.
Késői benyújtás:	Minden megkezdett nap után 5% levonás az elért eredményből (azaz pl. 5 nap késés után 100%-os leadandóra már csak max. 100% - 5x5% = 75%-ot lehet szerezni).
Értékelés:	0 – 50% - Elégtelen (1)
	51 – 60% - Elégséges (2)
	61 – 70% - Közepes (3)
	71 – 85% - Jó (4)
	86 – 100% - Jeles (5)
A formai követelmények tekintetében az alábbi linken elérhető útmutatót/sablont kell használni.

Feladat I. része

Rezisztencia és veszteség számítása végeselem-módszerrel

A kapott sorszám alapján a feladat geometriájának méreteit a következő táblázatban találja: Feladat #4 méretei.

A feladat: meghatározni a hőmérsékleteloszlást az elrendezés tetszőlegesen választott vezetőjében a veszteség 50 Hz-en és 500 Hz-en számolt értékének esetére.

Az anyagtulajdonságok.

Anyag	Réz	PVC
$$\rho~[\text{kg}/\text{m}^3]$$	8960	1380
$$c_{\text{P}}~[\text{J}/(\text{kg}\cdot\text{K})]$$	383	1172
$$\lambda~[\text{W}/(\text{m}\cdot\text{K})]$$	401	0,2

A FEMM szoftver esetében a térfogatra vonatkoztatott hőkapacitást (Volumetric heat capacity) kell megadni. Ezt a hőkapacitás (

$$c_{\text{P}}$$ ) és a sűrűség ( $$\rho$$ ) szorzata adja:

$$c_{\text{PV}} = c_{\text{P}} \cdot \rho$$ $$\Bigg[\frac{\text{J}}{\text{m}^3\cdot\text{K}}\Bigg]$$ .

Azonban mivel időben állandó feladatról van szó, ezért nem szükséges a megadása.

A feladat gerjesztése (

$$q_V$$ ) az egységnyi térfogatra vett veszteség, amit nem más, mint az örvényáram-veszteség és a vezető térfogatának hányadosa:.

$$q_V = \frac{P_{\text{ec}}}{V_{\text{vezető}}} \Bigg[\frac{\text{W}}{\text{m}^3}\Bigg]$$ ,

ahol

$$P_{\text{ec}}$$ az örvényáram okozta veszteség a vezetőben, $$V$$ pedig az egységnyi hosszú vezető térfogata.

A feladat külső felületére a peremfeltételnek hőszállítást (konvekciót) (Neumann-peremfeltétel) írunk elő:

$$-\lambda\cdot\frac{\partial T}{\partial n} = \alpha\cdot(T_{\text{külső}} - T)$$ ,

ahol

$$\lambda~\Big[\tfrac{\text{W}}{\text{m}\cdot\text{K}}\Big]$$ a hővezetési tényező, $$T_{\text{külső}}$$ a környezeti hőmérséklet és $$\alpha~\Big[\tfrac{\text{W}}{\text{m}^2\cdot\text{K}}\Big]$$ a hőátadási tényező. Ennél a feladatnál $$T_{\text{külső}} = 22°\text{C} = 295,15~\text{K}$$ és $$\alpha = 9~\tfrac{\text{W}}{(\text{m}^2\cdot\text{K})}$$ legyen, amit használunk. A valóságban $$\alpha$$ egy hőmérsékletfüggő paraméter.

A

$$z-$$ irányú hossza a feladatnak minden esetben $$1\,\text{m}$$ legyen és a szigetelő (PVC) vastagsága $$4,2\,\text{mm}$$ .

Elvégzendő feladatok

• A megadott paraméterek alapján elkészíteni a síkbeli (planar) feladat geometriáját a FEMM vagy Agros2D szoftverek valamelyikében;
• Az anyagtulajdonságok, a gerjesztés és a peremfeltételek megadása;
• A FEM szimuláció futtatása;
• Az eredmények kiértékelése:
  • Vezető átlaghőmérséklete 50 és 500 Hz esetében;
  • A vezető keresztmetszetében (pl. $$X = -20,2~\text{mm}~\dots~20,2~\text{mm}$$ ) a hőáramsűrűség kirajzoltatása.

A táblázatban található méretek jelentését az alábbi ábrák mutatják. A táblázatban a 2. oszlop jelöli a változat számát. A kapott feladat teljesen azonos a Feladat 4 esetében kapott feladattal.

Szoftverek használatának bemutatása

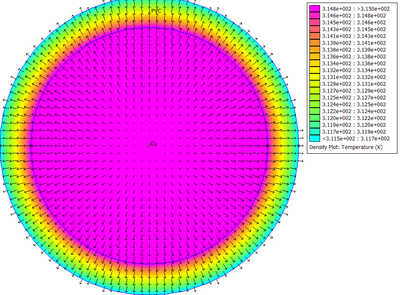
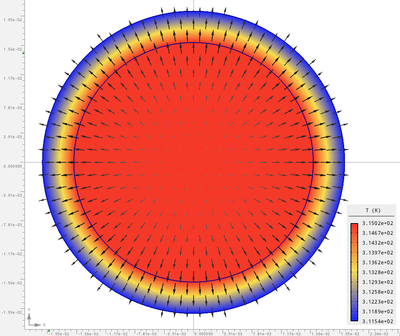
A Feladat 4-nél, az 1. ábrán látható elrendezésből a középső (

$$L_2$$ ) vezető szimulációján keresztül ismertetem az önálló feladat megoldásának menetét. A feladathoz készült videók segítségével elsajátítható a feladat beállítása, az anyagtulajdonságok, a peremfeltételek és a gerjesztés megadása. Majd a megoldást követően a térváltozók megjelenítése és a feladathoz kapcsolódó számítandó mennyiségek meghatározása.

Az eredmények összehasonlítása 50 Hz esetében. Szoftver FEMM Agros2D Veszteség [ $$\text{W}$$ ] 21,55 21,47 Hőmérséklet [ $$°\text{C}$$ ] 44,86 44,78

Az eredmények összehasonlítása 500 Hz esetében. Szoftver FEMM Agros2D Veszteség [ $$\text{W}$$ ] 63,47 63,20 Hőmérséklet [ $$°\text{C}$$ ] 89,33 89,06

FEMM - A hőmérsékleteloszlás és a hőáramsűrűség vektorok 50 Hz esetében.	Agros2D - A hőmérsékleteloszlás és a hőáramsűrűség vektorok 50 Hz esetében.

Videók a szoftverek használatához

• [ FEMM]
• [ Agros2D]

A hővezetés differenciálegyenlete^[1][2]

A hővezetés általános differenciálegyenletéhez az energimegmaradás tételét a hővezetés jelenségére alkalmazva jutunk.
Vizsgáljuk egy

$$V$$ térfogatú hővezető közeg energiaegyensúlyát. A térfogatba foglalt közeg:

$$m = \int_{V}\rho~\text{d}V$$ ,

ahol

$$\rho~\Big[\tfrac{\text{kg}}{\text{m}^3}\Big]$$ a sűrűség.
A tömeg hőmérsékletének $$\text{d}T$$ értékkel való növelése $$\text{d}\tau$$ idő alatt $$\text{d}Q$$ hőmennyiség közlése mellett történik. A hőmérséklet idő szerinti változása

$$\text{d}T = \frac{\partial T}{\partial \tau}~\text{d}\tau$$

egy helyfüggő érték. A felmelegítéshez szükséges hőmennyiség

$$\text{d}Q = \text{d}\tau\int_{V} c\cdot\rho\cdot\frac{\partial T}{\partial \tau}~\text{d}V$$ ,

ahol

$$c~\Big[\tfrac{\text{J}}{\text{kg}\cdot\text{K}}\Big]$$ az anyag helytől függő fajhője.

A közölt hőmennyiség származhat a vizsgált térrészen belül elhelyezkedő hőforrásból (

$$\text{d}Q_1$$ ), vagy érkezhet a vizsgált tartományt határoló felületen keresztül hővezetéssel ( $$\text{d}Q_2$$ ). A két hőmennyiség összege a felmelegítésre fordított hőmennyiséggel egyenlő:

$$\text{d}Q = \text{d}Q_1 + \text{d}Q_2$$ .

Hőforrásként jelentkezhet a közegben például az elektromos áram hőhatása. A hőforráseloszlás

$$\biggl(q_V~\Big[\tfrac{\text{W}}{\text{m}^3}\Big]\biggr)$$ ismeretében a vizsgált $$V$$ térrészben $$\text{d}\tau$$ idő alatt keletkező hőmennyiség:

$$\text{d}Q_1 = \text{d}\tau\int_{V} q_V~\text{d}V$$ .

A

$$V$$ térrészt határoló $$S$$ felületen át vezetéssel a térrészbe belépő és az onnan szintén vezetéssel kilépő hőmennyiség eredője, ugyancsak $$\text{d}\tau$$ idő alatt:

$$\text{d}Q_2 = -\text{d}\tau\int_{S} \vec{q}~\text{d}\vec{S}$$ ,

ahol

$$\vec{q}~\Big[\tfrac{\text{W}}{\text{m}^2}\Big]$$ a hőáramsűrűség vektora. Az $$S$$ felület normálisát pozitívnak tekintjük, ha a vizsgált térrészből kifelé mutat. A negatív előjel azért szükséges, mert a $$\text{d}Q_2$$ hőmennyiséget akkor tekintjük pozitívnak, ha az a vizsgált térrészben lévő tömeg hőmérsékletét növeli. Azonban a felület normálisának iránya miatt (kifelé mutat) a térrészbe belépő hőmennyiség negatív értéként adódik.

A hőmérsékletek azonosságát kifejező egyenletbe helyettesítve:

$$\text{d}\tau\int_{V} c\cdot\rho\cdot\frac{\partial T}{\partial \tau}~\text{d}V = \text{d}\tau\int_{V} q_V~\text{d}V -\text{d}\tau\int_{S} \vec{q}~\text{d}\vec{S}$$ .

Ez az összefüggés azt mutatja, hogy az

$$S$$ felület által határolt $$V$$ térfogatban lévő közeg belső energiájának a vizsgált $$\text{d}\tau$$ idő alatt történő megváltozása az $$S$$ felületen keresztül vezetéssel belépő ls kilépő hőmennyiségek eredőjéből, valamint a $$V$$ térfogaton belül elhelyezkedő hőforrás által szolgáltatott hőmennyiségből adódik.
A Gauss-Osztrogradszkij tétel értelmében a jobb oldal második tagja átalakítható:

$$\int_{S} \vec{q}~\text{d}\vec{S} = \int_{V} \nabla\cdot\vec{q}~\text{d}V$$ ,

amit visszahelyettesítve és átrendezve a következő egyenletre vezet:

$$\text{d}\tau\int_{V} c\cdot\rho\cdot\frac{\partial T}{\partial \tau}~\text{d}V = \text{d}\tau\int_{V} q_V~\text{d}V -\text{d}\tau\int_{V} \nabla\cdot\vec{q}~\text{d}V \rightarrow \text{d}\tau\int_{V} \big(c\cdot\rho\cdot\frac{\partial T}{\partial \tau} - q_V + \nabla\cdot\vec{q}\big)~\text{d}V = 0$$ .

Figyelembe véve azt, hogy az integrál zérus értéke az integrandusz zérus voltát jelenti, tehát

$$c\cdot\rho\cdot\frac{\partial T}{\partial \tau} - q_V + \nabla\cdot\vec{q} = 0$$ .

Egy szilárd testben, amelyben a hő kizárólag vezetés útján terjed, a

$$\vec{q}$$ hőáramsűrűség valamely helyen a hely környezetében uralkodó hőmérsékleteloszlás alapján megállapítható. A legnagyobb hőmérsékletváltozás irányába mutató gradiens vektor és a $$\vec{q}$$ hőáramsűrűség vektor iránya megegyezik. Azonban a tapasztalat szerint a hő mindig a csökkenő hőmérséklet irányába áramlik, tehát a a hőmérsékletgradiens vektor és a $$\vec{q}$$ hőáramsűrűség vektor értelme ellentétes. A hőáramsűrűség vektor abszolút értéke az egységnyi elmozdulásra jutó hőmérsékletcsökkenéssel , azaz a gradiens vektor abszolút értékével arányos. A kettő közötti arányossági tényező az adott anyag $$\lambda~\Big[\tfrac{\text{W}}{\text{m}\cdot\text{K}}\Big]$$ hővezetési tényezője. A leírtak alapján, az úgynevezett Fourier-törvény:

$$\vec{q} = \lambda\cdot(-\nabla~T) = -\lambda\cdot \nabla~T$$ .

Ezt az összefüggést felhasználva a hővezetés általános differenciálegyenlete:

$$-\nabla(\lambda\cdot \nabla~T) + c\cdot\rho\cdot\frac{\partial T}{\partial \tau} = q_V$$ .

További egyszerűsítést jelent az esetünkben, hogy stacionárius hőáramlásról van szó, azaz nincs időbeli változás

$$-\nabla(\lambda\cdot \nabla~T) = q_V$$ .

A feladatmegoldás során ezt a Poisson-egyenletet oldjuk meg, ahol

$$q_V~\Big[\tfrac{\text{W}}{\text{m}^3}\Big]$$ az adott térfogatban keletkező veszteség.

Feladat II. része

A műszaki jelentés elkészítése és leadása a Moodle rendszerben PDF formátumban.
A műszaki jelentés a következő linken elérhető: Word; PDF.

Hivatkozások

1. Jump up ↑ Szabó I., Áramlástan, műszaki hőtan, Tankönyvkiadó, Budapest, 1973.
2. Jump up ↑ Imre L., Villamos gépek és eszözök melegedése és hűtése - 2. Bevezetés a hőátviteli folyamatok elméletébe, Műszaki Könyvkiadó, Budapest, 1982.