Difference between revisions of "3. lecke példája"
(→A megoldó beállítása, a szimuláció futtatása) |
(→A megoldó beállítása, a szimuláció futtatása) |
||
| Line 49: | Line 49: | ||
A megoldónál definiálni kell az időtartomány végét, ameddig futtani szeretnénk a szimulációt, valamint az időlépést. Ennél a példánál 15 ms legyen az időtartomány vége (''Stop time'') és 0,05 ms (periodusonként 100 időlépés) az időlépés (''Time step''). | A megoldónál definiálni kell az időtartomány végét, ameddig futtani szeretnénk a szimulációt, valamint az időlépést. Ennél a példánál 15 ms legyen az időtartomány vége (''Stop time'') és 0,05 ms (periodusonként 100 időlépés) az időlépés (''Time step''). | ||
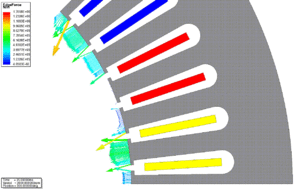
| − | Itt már szükség lehet a nemlineáris megoldó beállításaira is, mivel az állórészt és forgórészt alkotó acél mágnesezési görbéje (<math>\vec{B} - \vec{H}</math> kapcsolat) nemlineáris. Erre jó példa a lenti ''K ábra'', ahol látható, hogy milyen nagy mértékben különbözhet helyről-helyre a relatív permeabilitás értéke. | + | Itt már szükség lehet a nemlineáris megoldó beállításaira is, mivel az állórészt és forgórészt alkotó acél mágnesezési görbéje (<math>\vec{B} - \vec{H}</math> kapcsolat) nemlineáris. Erre jó példa a lenti ''K. ábra'', ahol látható, hogy milyen nagy mértékben különbözhet helyről-helyre a relatív permeabilitás értéke. |
Ahhoz, hogy a szimuláció lefutását követően több időpillanatban megjelenítsük az eredményt, szükség van megadni, melyik időlépésben szeretnénk a megoldást elmenteni. Ha ezt nem tesszük meg, automatikusan az utolsó időlépést menti el, ebben az időpillanatban lehet a térváltozókat (<math>\vec{A}; \vec{B}; \vec{H}</math>; ...) és az azokból származtatott mennyiségeket (<math>\text{veszteség}, \text{energia}, ...</math>) megjeleníteni. | Ahhoz, hogy a szimuláció lefutását követően több időpillanatban megjelenítsük az eredményt, szükség van megadni, melyik időlépésben szeretnénk a megoldást elmenteni. Ha ezt nem tesszük meg, automatikusan az utolsó időlépést menti el, ebben az időpillanatban lehet a térváltozókat (<math>\vec{A}; \vec{B}; \vec{H}</math>; ...) és az azokból származtatott mennyiségeket (<math>\text{veszteség}, \text{energia}, ...</math>) megjeleníteni. | ||
Revision as of 07:10, 8 March 2019
|
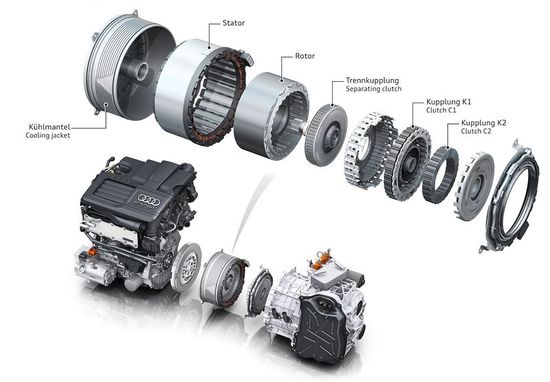
Állandó mágneses motor | |
| Audi A3 Sportback e-tron hajtásláncának meghajtó egysége. [1] | Állandó mágneses szinkron motor üzem közben. [Kattints a képre az animáció megtekintéséhez]. |
|
Oktató
|
További oktatók:
|
Contents
A feladat célja
A hallgató megismerje a végeselem-módszer főbb lépéseit, mint a modell előkészítése (geometria elkészítése vagy importálása), anyagparaméterek, peremfeltételek és gerjesztés megadása egy időfüggő szimuláción keresztül. Elősegítse a villamos forgógépekben jelentkező jelenségek - zaj, rezgés, melegedés - forrásának megértését.
A feladat megoldásához szükséges ismeretek
- A végeselem-módszer lépései;
- Az időben változó mágneses térre vonatkozó elméleti ismeretek (anyagok definiálásához, gerjesztés megadásához);
- Alapvető ismeretek a villamos gépek működéséről.
A feladat megoldásának lépései
Az ANSYS Electronics Desktop elindítását követően a File [math]\to[/math] Open almenü segítségével nyissuk meg a PM_Motor_Oktatas.aedt fájlt.
Az ANSYS Maxwell használatához a Help menüje és a YouTube-on fellelhető videók sok segítséget nyújtanak.
A feladat definiálása
Ebben az esetben a feladat geometriája és a feladat definiálása előre elkészített. Ennek oka, a hosszadalmas beállítás elkerülése és az, hogy alapvetően a példa azt a célt szolgálja, hogy a nemkívánatos jelenségek forrásait (erő, veszteség) áttekintsük egy villamos forgógép példáján.
A futtatás előtt és közben röviden áttekintjük a feladat beállításait.
Fontos megjegyezni, hogy az előző két példa esetében az adaptív hálozó finomította a felbontást. Azonban időfüggő (tranziens) esetben nincs lehetőség az adaptív hálózó használatára, így nekünk kell előre definiálni a feladat felbontását különböző hálózási műveletekkel.
A megoldó beállítása, a szimuláció futtatása
A megoldónál definiálni kell az időtartomány végét, ameddig futtani szeretnénk a szimulációt, valamint az időlépést. Ennél a példánál 15 ms legyen az időtartomány vége (Stop time) és 0,05 ms (periodusonként 100 időlépés) az időlépés (Time step).
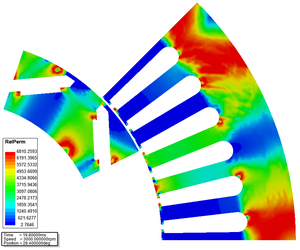
Itt már szükség lehet a nemlineáris megoldó beállításaira is, mivel az állórészt és forgórészt alkotó acél mágnesezési görbéje ([math]\vec{B} - \vec{H}[/math] kapcsolat) nemlineáris. Erre jó példa a lenti K. ábra, ahol látható, hogy milyen nagy mértékben különbözhet helyről-helyre a relatív permeabilitás értéke.
Ahhoz, hogy a szimuláció lefutását követően több időpillanatban megjelenítsük az eredményt, szükség van megadni, melyik időlépésben szeretnénk a megoldást elmenteni. Ha ezt nem tesszük meg, automatikusan az utolsó időlépést menti el, ebben az időpillanatban lehet a térváltozókat ([math]\vec{A}; \vec{B}; \vec{H}[/math]; ...) és az azokból származtatott mennyiségeket ([math]\text{veszteség}, \text{energia}, ...[/math]) megjeleníteni.
Az eredmények kiértékelése
A példa célja bemutatni a villamos gépek nemkívánatos jelenségeinek forrását. A melegedés forrása a gép különböző részeiben keletkező veszteség. Az örvényáram veszteséggel az előző leckében már találkoztunk. Azonban az úgynevezett elektromos acéloknál több összetevője van a vasveszteségnek
[math] p_{\text{vas}} = p_{\text{h}} + p_{\text{c}} + p_{\text{e}} = K_{\text{h}}f(B_{\text{max}})^2 + K_{\text{c}}(f B_{\text{max}})^2 + K_{\text{e}}(f B_{\text{max}})^{1.5} [/math],
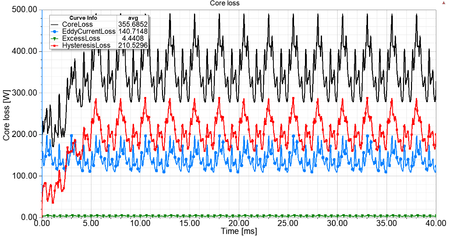
ahol [math]p_{\text{h}}[/math] a hiszterézis veszteség, [math]p_{\text{c}}[/math] az örvényáram veszteség, [math]p_{\text{e}}[/math] a járulékos veszteség, [math]K_{\text{h}}, K_{\text{c}}, K_{\text{e}}[/math] a veszteségekhez tartozó együttható, [math]f[/math] a frekvencia és [math]B_{\text{m}}[/math] a mágneses fluxussűrűség maximuma. A B ábra a vasveszteséget és az összetevőit mutatja az idő függvényében.
Az [ ANSYS Maxwell] automatikusan kiszámítja a veszteségeket a feladatban, azonban ha arra vagyunk kíváncsiak, egy-egy térrészben (pl. az öntöttvas rúdban) mekkora az örvényáram okozta veszteség, akkor azt nekünk kell kiszámolni a Calculator (Maxwell 3D [math]\to[/math] Fields [math]\to[/math] Calculator...) segítségével. Az örvényáramú veszteség a következő összefüggéssel számítható
[math] P_{ö} = \frac{1}{2}\int_{V} \vec{J}\cdot\vec{E}^{*}\,\text{d}V = \int_{V} \frac{\vec{J}\cdot\vec{J}^{*}}{2\sigma}\,\text{d}V[/math] [W].
Azonban a fenti összefüggés helyett a Calculator-ban a következő lépéseket kell elvégezni
- Input [math]\to[/math] Quantity [math]\to[/math] OhmicLoss
- Input [math]\to[/math] Geometry [math]\to[/math] Itt kiválasztjuk a térfogatot, ahol számolni szeretnénk a veszteséget
- Scalar [math]\to[/math] [math]\int[/math] (Integrálás)
- Output [math]\to[/math] Eval
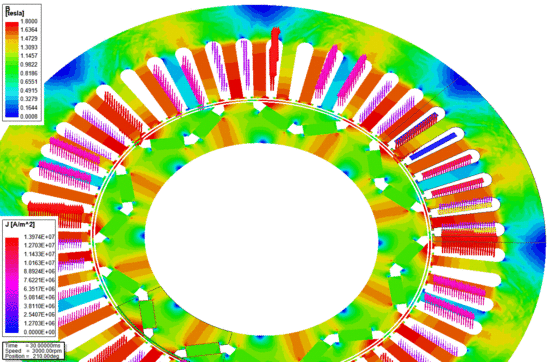
A térváltozók is megjeleníthetőek különböző formában erre mutat egy-egy példát a következő két ábra.
| B. ábra - A vasveszteség és annak összetevői az idő függvényében. | K. ábra - A relatív permeabilitás az álló- és forgórészben. | J. ábra - A fogerő változása az idő függvényében [Kattints a képre az animáció megtekintéséhez]. |