Difference between revisions of "Mágneses kör"

Revision as of 17:04, 19 March 2022 (view source) Marcsa (talk | contribs) (→‎A feladat megoldásához szükséges ismeretek) ← Older edit		Revision as of 17:06, 19 March 2022 (view source) Marcsa (talk | contribs) (→‎A feladat megoldásához szükséges ismeretek) Newer edit →
Line 38:		Line 38:
	|-		|-
	| style="background: #D5E0EE;" | '''Hónap'''		| style="background: #D5E0EE;" | '''Hónap'''
−	| '''Nap'''	+	| style="background: #D5E0EE;" | '''Nap'''
−	| '''Hét'''	+	| style="background: #D5E0EE;" | '''Hét'''
−	| '''Téma'''	+	| style="background: #D5E0EE;" | '''Téma'''
−	| '''Házi feladat'''	+	| style="background: #D5E0EE;" | '''Házi feladat'''
−	| '''Infó'''	+	| style="background: #D5E0EE;" | '''Infó'''
	|- valign=top		|- valign=top
	| rowspan=3 style="text-align: center;" | Február		| rowspan=3 style="text-align: center;" | Február
−	| 11.	+	| style="background: #ACC0DD;" | 11.
−	| 1.	+	| style="background: #ACC0DD;" | 1.
−	| [https://drive.google.com/file/d/1_ts7I08AS1rv-gjUmKuy7x6jeUzlovCh/view?usp=sharing ''Elméleti alapok ismétlése (Villamosságtan, Elektrodinamika)'' - ''Opcionális'']	+	| style="background: #ACC0DD;" | [https://drive.google.com/file/d/1_ts7I08AS1rv-gjUmKuy7x6jeUzlovCh/view?usp=sharing ''Elméleti alapok ismétlése (Villamosságtan, Elektrodinamika)'']
−	| -	+	| style="background: #ACC0DD;" | -
−	| -	+	| style="background: #ACC0DD;" | '''Opcionális'''
	|- valign=top		|- valign=top
	<!-- column 3 of this row occupied by cell F (to the left) -->		<!-- column 3 of this row occupied by cell F (to the left) -->

---

Revision as of 17:06, 19 March 2022

Mágneses körök - Fejlesztés alatt
A feladat végeselemhálója és a peremek elnevezése.	A feladat megoldása ONELAB (Gmsh + GetDP) segítségével.
Oktató Marcsa Dániel (óraadó) Előadás: - Fogadóóra: egyeztetés alapján	További oktatók: - Fogadóóra: -.

A feladat célja

Ennek a lapnak a célja a mágneses körök ekvivalensének rövid bemutatása és a vele való számítás ismertetése. A mágneses kör számítása több példán keresztül kerül bemutatásra. Az eredmények ellenőrzése végeselem-módszerrel történik, azon belül ANSYS Maxwell szoftverrel. A végeselem-módszerrel megoldott példák közül néhányhoz videó is készül a megoldás menetéről.

Az itt bemutatott példák közül az FGY-vel jelölt példák Fodor György - Villamosságtani példatár IV., Mágneses terek - Térbeli áramlás, Tankönyvkiadó, 1963 könyvből származnak.

A feladat megoldásához szükséges ismeretek

• Sztatikus mágneses terek;
• A végeselem-módszer lépései és annak elméleti háttere.

Hónap	Nap	Hét	Téma	Házi feladat	[Collapse] Infó
Február	11.	1.	Elméleti alapok ismétlése (Villamosságtan, Elektrodinamika)	-	Opcionális
	18.	2.	Transzformátor - Elmélet	Házi feladat - I.	-
	25.	3.	Transzformátor - Gyakorlat	-	-
Március	04.	4.	Villamos forgógépek alapjai	-	1. zárthelyi
	18.	5.	Egyenáramú gép - Elmélet	Házi feladat - II.	-
	25.	6.	Egyenáramú gép - Gyakorlat	-	-
Április	01.	7.	Váltakozó áramú mezők	Házi feladat - III.	-
	08.	8.	[ Aszinkron gép - Elmélet]	-	[ 2. zárthelyi] Terhelt állapot Jelleggörbéje
	22.	9.	Aszinkron gép - Gyakorlat	-	-
	29.	10.	[ Szinkron gép - Elmélet]	Házi feladat - IV.	[ 3. zárthelyi] Működés szemléltetése
Május	06.	11.	Szinkron gép - Gyakorlat	-	-
	13.	14.	[ Villamos gépek és hajtások EMC-s problémái]	-	Látókör szélesítése

A mágneses kör

A feladat részletes definiálása a videóban is megtalálható. Emellett készítettem egy háromdimenziós ábrát az elrendezés könnyebb elképzeléséhez és annak méretekkel ellátott keresztmetszetét. A feladat az eltolási szimmetria (

$$Z$$ -tengely mentén nem változik a feladat, vagyis $$\partial/\partial z = 0$$ ) miatt kétdimenziós feladatnak tekinthető. Emellett a geometria jelölt középvonalára is szimmetrikus az elrendezés, így elég a felét vizsgálni. Ezen túl pedig a fém részek elhagyhatók, mert ott az elektromos térerősség értéke nulla. Így elegendő a két fémrész közötti teret kitöltő $$2.4\cdot\varepsilon_0$$ permittivitású anyagot vizsgálni a megfelelő peremfeltételekkel. Dirichlet-típusú peremfeltételként adjuk meg a külső és belső elektróda potenciálját (külső - $$0~\text{V}$$ ; belső - $$100~\text{V}$$ ). A szimmetriasík Neumann-típusú peremfeltétel lesz, viszont ez előírás nélkül, automatikusan is teljesül jelen feladatnál.

A feladat megoldásához a Laplace-egyenletet oldjuk meg

$$-\,\text{div}\,\varepsilon\,\text{grad}\varphi = 0$$

ahol

$$\varphi$$ az elektromos skalárpotenciál, a következő peremfeltételekkel

$$\Gamma_{\text{D}1} = 0~\text{V}$$ ,

$$\Gamma_{\text{D}2}= 100~\text{V}$$ ,

$$\Gamma_{\text{N}}= \frac{\partial \varphi}{\partial n} = 0$$ (homogén Neumann-peremfeltétel).

A szimulációval kapott eredmények

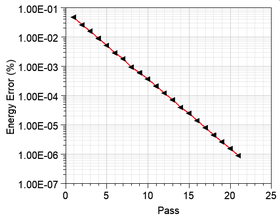
Az előbb megadott parciális differenciálegyenlet és peremfeltételekkel előálló feladat megoldásával a következő táblázatban összefoglalt eredmények születtek a kapacitás értékére. A Matlab PDE Toolbox megoldása az előadásból (Gyimóthy Szabolcstól) származik. Gyakorlatilag az összes szoftver azonos megoldásra vezetett. Ilyen szempontból sokkal érdekesebb a végeselemek száma. Az ANSYS Maxwell és 2D Extarctor esetében jelentősen kevesebb a végeselemek száma, mint a többi esetben. Ennek oka az adaptív hálósűrítés^[1], amit a két Ansys szoftver alkalmaz az elektrosztatika példák esetében. Ennek köszönhetően ott lesz sűrűbb a felbontás, ahol az szükséges. Az adaptív hálósűrítésre mutat példát a jobb oldali ábra. Alatta pedig a feladat teljes tartományára számított (globális) hiba változása látható.

A vizsgált elrendezés kapacitása.

	Matlab PDE Toolbox	ONELAB	Maxwell 2D	2D Extractor	FEMM	Agros2D
Végeselemek száma	2944	2598	740	258	7885	2432
Kapacitás [ $$\text{pF/m}$$ ]	173.51	173.78	173.33	173.29	173.70	173.64

Mindegyik esetben lineáris háromszög elemekkel lett felbontva a vizsgált tartomány. A lineáris végeselemekből következik, hogy a végeselemen belül a

$$\varphi$$ potenciál értéke lineárisan változik, vagyis az elektromos térerősség ( $$\vec{E}=\text{grad}\varphi$$ ) konstans a végeselemen belül. Ez jól megfigyelhető az alábbi két ábrán. A baloldali ábrán a kapott skalárpotenciálból számított elektromos térerősség euklideszi normája látható. A jobb oldali ábrán pedig ugyanez az eredmény a simítást (smoothing) követően.

• Az elektromos térerősség a vizsgált elrendezésben.
• 

  Lineáris közelítés esetén.

• 

  A simítást követően.

Legvégül egy-egy ábra az elektromos skalárpotenciálról és az elektromos térerősség vektorairól. Az elektromos skalárpotenciál ábráján jól láthatóak a vezető körül kialakuló ekvipotenciális vonalak. A vektorok esetében jól látható a homogén Neumann-peremfeltétel teljesülése a szimmetrisík mentén.

Az elektromos skalárpotenciál értéke az elrendezésben.	Az elektromos térerősség vektorai az elrendezésben.

References

1. Jump up ↑ Gyimóthy Sz.: Adaptív automatikus hálógenerálás a végeselem módszerhez, PhD disszertáció, 2003.