4. lecke

Integrálegyenleteken alapuló módszerek / Hullámegyenlet
Oktató Marcsa Dániel (óraadó) Előadás: - Fogadóóra: egyeztetés alapján	További oktatók: - Fogadóóra: -.

Integrálegyenleten alapuló módszerek

Peremelem módszer (Boundary Element Method - BEM)

Peremelem módszeren (BEM - Boundary Element Method) alapuló megoldók többsége a momentumok módszerét (MoM - Method of Moments) használja, hogy megoldja az EFIE (Electric Field Integral Equation), az MFIE (Magnetic Field Integral Equation) vagy a CFIE (Combined Field Integral Equation) egyenletrendszert, az elektromos és/vagy mágneses áramokat meghatározzásához az egymástól eltérő anyagok közötti határfelületen. Emiatt sok esetben az EM szimulációs programot csak "momentumok módszerén" alapuló szoftverként jellemzik, holott a peremelem módszert használja.

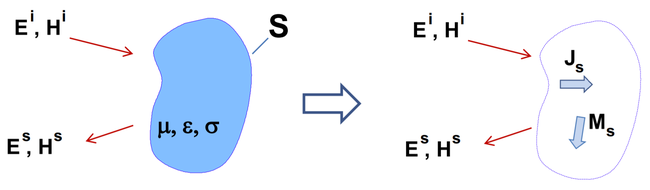
1. ábra - Az egyenértékűség elve.

A peremelem módszer első lépése a probléma geometriájának leírása az azzal egyenértékű felületi áramok eloszlásaként homogén közegben (általában szabad térben). Amint az 1. ábrán látható, az objektum körüli tér az objektumra beeső térből, az objektumról visszavert térből és az objektumból származó térből áll össze. Az egyenértékűségi tétel azt állítja, hogy az objektumon kívüli téreloszlás pontosan leírható, ha eltávolítja az objektumot, és azzal egyenértékű elektromos és mágneses áramokkal helyettesítjük a határfelületen.

Mivel a peremelem módszernél is használt EFIE és MFIE sémák az árameloszlás esetében csak a homogén közegben érvényesek, a feladatban lévő összes objektumot el kell távolítani, és a határaiknak megfelelő (kezdetben ismeretlen) felületi áramokkal kell helyettesíteni.

Az alábbi egyenletek az EFIE és MFIE általános alakját mutatják, ahogy a peremelem módszert használó programok jellemzően alkalmazzák, amelyek csak fémes tárgyakat modelleznek (azaz nincs ekvivalens mágneses felületi áram);

[math]\vec{E}(\vec{r})=\frac{-j\eta}{4\pi k}\int_S\vec{J}_S(\vec{r}')\cdot\vec{G}_e(\vec{r},\vec{r}')\text{d}S'[/math]

[math]\vec{H}(\vec{r})=\frac{1}{4\pi}\int_S\vec{J}_S(\vec{r}')\times\nabla'\vec{G}_m(\vec{r},\vec{r}')\text{d}S'[/math]

Ezekben az egyenletekben a [math]\int_S \text{d}S'[/math] felületre vett integrál az összes határfelületre vett integrálást jelenti. Azt érdemes figyelembe venni, hogy perem csak olyan helyeken létezik, ahol két különbőző anyag között határfelület van, tehát a perem mérete korlátozott (azaz nincs integrálás a végtelenbe).

The functions [math]\vec{G}_e[/math] and [math]\vec{G}_m[/math] in these equations relate source currents to the electric and magnetic field generated by those currents, respectively. [math]\vec{G}_e[/math] and [math]\vec{G}_m[/math] are called Green's functions and they play a central role in boundary element analysis. Free-space Green's functions express the field emanating from the surface current represented by an individual basis function (e.g. the current on an individual surface patch). However, other Green's functions can be employed to express the field emanating from more complex structures that are common to a particular problem geometry. For example, a geometry consisting of metal surfaces coated with a thin dielectric may employ a special Green's function that expresses the fields emanating from the combined surfaces of the metal-dielectric and dielectric-air interfaces. This can substantially reduce the number of surface elements required to model the problem.

All Green's functions are approximate expressions that are accurate for a limited range of frequencies, distances and source geometries. Many boundary element methods employ several Green's functions to model different regions of a problem or different problem environments.

General purpose 3D BEM codes usually employ basis and weighting functions that are linear current distributions on a rectangular or triangular surface patch. There are generally two unknowns per patch corresponding to two orthogonal current vectors. Thin wires can be represented very efficiently with a single unknown representing the amplitude of the current distribution on each wire segment.

Point matching techniques employ basis and weighting functions that are simple impulse functions often at the center of each patch or segment. Pulse matching techniques employ basis and weighting functions that have a constant value everywhere on the patch or segment. More accurate implementations employ basis and weighting functions that transition smoothly from one patch to the next. Rao-Wilton-Glisson (RWG) basis functions are a popular choice for codes that employ triangular surface patch elements. Roof-top basis functions are often employed by codes that use rectangular elements.

Generally, CEM software employing a boundary element method excels at modeling unbounded problems, particularly when it is not necessary to model regions of great complexity in detail. Structures that can be adequately represented with a wire grid can be analyzed very effectively using boundary element methods, because these methods model wires very efficiently.

Following table lists various strengths and weakness of BEM modeling techniques. Note that the capabilities of any particular modeling software depend strongly on the form of the integral equation solved, the choice of basis and weighting functions, the Green's function(s) employed, and the matrix solver and any optimization techniques employed.

Momentumok módszere (Method of Moments - MoM)

In the 1960s, R.F. Harrington and others applied a technique called the Method of Moments to the solution of electromagnetic field problems. The Method of Moments (also called the Method of Weighted Residuals) is a technique for solving linear equations of the form,

[math]\mathcal{L}(\phi)=f[/math]

where the functional [math]\mathcal{L}(\bullet)[/math] is a linear operator, [math]f[/math] is a known excitation or forcing function, and [math]\phi[/math] is an unknown quantity. To solve this problem on a digital computer, we start by expressing the unknown solution as a series of basis or expansion functions, [math]v_n[/math],

[math]\phi = \sum_{n=1}^{N}a_n v_n[/math]

where [math]a_n[/math] are unknown coefficients describing the amplitude of each term in the series.

Now instead of one equation with a continuous unknown quantity, [math]f[/math], we have an equation with [math]N[/math] scalar unknowns,

[math]\mathcal{L}(a_1v_1+a_2v_2+\dots+a_Nv_N)=f[/math].

To solve for the values of [math]a_n[/math], we need [math]N[/math] linearly independent equations; so [math]a_n[/math] different weighting or testing functions, [math]w_n[/math], are applied. This yields the following system of [math]N[/math] equations in [math]N[/math] unknowns:

[math] \begin{bmatrix} \langle w_1,\mathcal{L}(v_1)\rangle & \langle w_1,\mathcal{L}(v_2)\rangle & \cdots & \langle w_1,\mathcal{L}(v_N)\rangle \\ \langle w_2,\mathcal{L}(v_1)\rangle & \langle w_2,\mathcal{L}(v_2)\rangle & \cdots & \langle w_2,\mathcal{L}(v_N)\rangle \\ \vdots & \ddots & \vdots \\ \langle w_N,\mathcal{L}(v_1)\rangle & \langle w_N,\mathcal{L}(v_2)\rangle & \cdots & \langle w_N,\mathcal{L}(v_N)\rangle \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_N \end{bmatrix} = \begin{bmatrix} \langle w_1, f_1 \rangle \\ \langle w_2, f_2 \rangle \\ \vdots \\ \langle w_N, f_N \rangle \end{bmatrix} [/math]

A fenti összefüggés lineáris egyenletrendszerként a következő lesz

[math]\textbf{A}\textbf{x}=\textbf{b}[/math]

where the elements of [math]\textbf{A}[/math] are known quantities that can be calculated from the linear operator, the functional [math]\mathcal{L}(\bullet)[/math], and the chosen basis and weighting functions. The elements of \textbf{b} are determined by applying the weighting functions to the known forcing function. The unknown elements of [math]\textbf{x}[/math] can be found by solving the matrix equation. After solving for [math]\textbf{x}[/math] (i.e. the unknown coefficients, [math]a_n[/math]), the value of [math]\phi[/math] is determined using [math]\phi = \sum_{n=1}^{N}a_n v_n[/math] equation.

The Method of Moments (MoM) can be used to solve a wide range of equations involving linear operations including integral and differential equations. This numerical technique has many applications other than electromagnetic modeling; however the MoM is widely used to solve equations derived from Maxwell's equations. In general, moment method codes generate and solve large, dense matrix equations and most of the computational resources required are devoted to filling and solving this matrix equation. The particular form of the equations that is solved and the choice of basis and weighting functions have a great impact on the size of this matrix and ultimately the suitability of a given moment method code to model a given geometry.

Equation Options

The most common equation form solved by CEM modeling codes based on the Method of Moments is the Electric Field Integral Equation (EFIE). This is an equation of the form,

[math]\vec{E}=f_e(\vec{J},\vec{M})[/math],

where [math]\vec{E}[/math] is the impressed (i.e. source) electric field and [math]\vec{J}[/math] and [math]\vec{M}[/math] are the induced electric and magnetic current densities, respectively. The EFIE will be discussed further in the section describing the Boundary Element Method. Generally, codes that solve a form of the EFIE excel at modeling open (unbounded) geometries in which the electric field dominates in the near-field region of the source.

Another equation solved by Moment Method codes is the Magnetic Field Integral Equation (MFIE), which has the general form,

[math]\vec{H}=f_m(\vec{J},\vec{M})[/math],

where [math]\vec{H}[/math] is the impressed (i.e. source) magnetic field intensity. Codes that solve a form of the MFIE are best suited for modeling geometries with circulating currents, where the magnetic near field is dominant.

Moment Method codes based on the EFIE or MFIE alone, may exhibit unstable behavior when the modeling surfaces form a resonant cavity at a particular frequency. To avoid this, many moment method codes solve a linear combination of the EFIE and MFIE known as a Combined Field Integral Equation (CFIE). This requires more calculations to fill the matrix, but results in a more stable solution when the modeling surface is large enough to support an interior resonance.

Some CEM modeling codes employ the Method of Moments to solve other equations. For example, static modeling codes often solve a form of Laplace's equation relating electric field strengths to charge densities or magnetic field strengths to current densities. The Generalized Multiple Technique (GMT), which is described in another section of this report, employs a moment method to solve equations for the electric field generated by multipole sources.

Bázis- és súlyfüggvény

A bázis- és a súlyfüggvény megfelelő választása óriási különbséget eredményezhet az elfogadható pontosságú megoldáshoz szükséges [math]N[/math] elemek számában. Mivel a megoldást a bázisfüggvények összegzésével kapjuk, fontos olyan bázisfüggvényt választani, amelyek kis szám esetében is pontosan leírja a megoldást. Például, amikor a felületi árameloszlást számoljuk, a bázisfüggvényeknek olyan árameloszlást leíró elemeknek kell lenniük, amelyeket összegezve megfelelően közelíteni a feladatban fellépő lehetséges árameloszlásokat.

Súlyfüggvénynek olyan kell választani, ami maximalizálja az egyenlet különböző súlyozott formáinak lineáris függetlenségét. Gyakran a legjobb, ha a bázisfüggvénnyel azonos súlyfüggvényt választunk. A momentumok módszer technikáinál is, ha a bázisfüggvény és a súlyfüggvény azonosak azt Galjorkin-módszernek nevezzük.

Hullámegyenlet

Itt a közvetlenül elektromos és mágneses térből előálló frekvenciatratománybeli egyenletekkel foglalkozunk. Ezeket szintén a Maxwell-egyenletekből kapjuk, amelyek mind az elektromos, mind a mágneses teret tartalmazza, amíg a hullámegyenlet mindig csak az egyik mennyiséget tartalmazza.

Hullámegyenlet

Az [math]\vec{E}[/math] elektromos térerősségre a hullámegyenletet kapjuk, ha kiküszöböljük a [math]\vec{H}[/math] mágneses térerősséget a I. és II. Maxwell-egyenletből a konstitúciós relációk segítségével. Ezt megtéve az elektromos térerősségre a hullámegyenlet

[math]\nabla\times\left(\frac{1}{\mu}\nabla\times\vec{E}\right)-\omega^{2}\varepsilon\vec{E}=-j\omega\vec{J}[/math].

Hasonlóképpen, az [math]\vec{E}[/math] elektromos térerősség kiküszöbölésével a mágneses térerősségre a hullámegyenlet

[math]\nabla\times\left(\frac{1}{\varepsilon}\nabla\times\vec{H}\right)-\omega^{2}\mu\vec{H}=\nabla\times\left(\frac{1}{\varepsilon}\vec{J}\right)[/math].

Ezeket az egyenleteket inhomogén hullámegyenletnek nevezzük. Az [math]\vec{E}[/math]-re kifejezett hullámegyenlet megoldása kielégíti a Gauss-törvényt és ugyanígy a [math]\vec{H}[/math]-ra kifejezett hullámegyenlet megoldása kielégíti a fluxusmegmaradás törvényét.